Arithmetic Progression-MCQ

Class X Math
MCQ for Quadratic Equations
1.    Every quadratic polynomial can have at most
        (a) three zeros
(b) one zero
        (c) two zeros
(d) none of these
2.    If x2 + 5px + 16 has no real roots, then
        (a)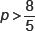
(b)
        (c)
(d) none of these
3.    For ax2 + bx + c = 0, which of the following statement is wrong?
        (a) If b2 – 4ac is a perfect square, the roots are rational.
        (b) If b2 = 4ac , the roots are real and equal.
        (c) If b2 – 4ac is negative, no real roots exist.
        (d) If b2 = 4ac , the roots are real and unequal.
4.    The roots of the equation 9x2 – bx + 81 = 0 will be equal, if the value of b is
        (a) ± 9
(b) ± 18
        (c) ± 27
(d) ± 54
5.    Which of the following is not a quadratic equation?
        (a) 3x2 – 5x + 9
(b)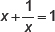
        (c) x2 – 9x = 0
(c)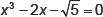
6.    For what value of t is 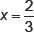a solution of 7x2 + tx – 3 = 0
        (a) –6
(b)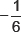
        (c)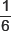
(d) 6
7.    The value of p for equation 2x2 – 4x + p = 0 to have real roots will be
        (a) p ≤ –2
(b) p ≥ 2
        (c) p ≤ 2
(d) p ≥ –2
8.    Which of the following has real roots?
        
9.    If p = 1 and q = –2 are roots of equation x2 – px + q = 0 , then quadratic equation will be
        (a) x2 + 2x –1= 0
(b) x2 – x – 2 = 0
        (c) x2 – 2x + 1= 0
(d) x2 + x + 2 = 0
10.    Roots of quadratic equation x2 – 3x = 0 , will be
           (a) 3
(b) 0, –3
           (c) 0, 3
(d) none of these
11.    Value of D when root of ax2 + bx + c = 0 are real and unequal will be
           (a) D ≥ 0
(b) D > 0
           (c) D < 0
(d) D = 0
12.    If px2 + qx + r = 0 has equal roots, value of r will be
           (a)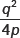
(b)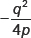
           (c)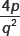
(d) none of these
13.    Positive value of p for which equation x2 + px + 64 = 0 and x2 – 8x + p = 0 will both have real roots will be
           (a) p ≥ 16
(b) p ≤ 16
           (c) p = 16
(d) none of these
14.    If equation 9x2 + 6px + 4 = 0 has equal roots, then both roots are equal to
           
15.    If the equation x2 – kx + 1, have no real roots, then
           (a) –2 < k < 2
(b) –3 < k < 3
           (c) k > 2
(d) k < –2
Answers