Introduction to Trigonometry-NCERT Solutions
Class X Math
NCERT Solution for Intorudction to Trigonometry
NCERT Solution for Intorudction to Trigonometry
1. In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) Sin A, cos A (ii) sin C, cos C
Sol. In right ΔABC, we have:
p = 24 cm, b = 7 cm
2. In the figure, find tan P – cot R.
Sol. In right ΔPQR, using the Pythagoras theorem, we get
3. If sin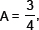 
calculate cos A and tan A.
calculate cos A and tan A.Sol. Let us consider, the right ΔABC, we have
Perp. = BC and Hyp. = AC
4. Given 15 cot A = 8, find sin A and sec A.
Sol. Let in the right ΔABC, we have
15 cot A = 8
Now, using Pythagoras theorem, we get
5. Given 
calculate all other trigonometric ratios.
calculate all other trigonometric ratios.Sol. Let us have a right ΔABC in which ∠B = 90°
6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Sol. Let us consider a right ΔABC,
7. 
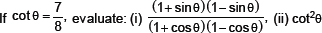
Sol. Let us have a right ΔABC in which ∠B = 90°, and ∠A = θ
8. If 3 cot A = 4, check whether 
Sol. Let us consider a right angled ΔABC in which ∠B = 90°
∴For ∠A, we have:
Base = AB and Perpendicular = BC. Also Hypotenuse = AC
3 cot A = 4
9. In triangle ABC, right-angled at B, if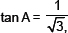 
find the value of:
find the value of: (i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C
Sol. Let us consider a right ΔABC, in which ∠B = 90°
For ∠A, we have
Base = AB
Perpendicular = BC
Hypotenuse = AC
10. In ΔPQR, right-anlged at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Sol. It is given that PQR is a right Δ, such that ∠Q = 90°
PR + QR = 25 cm
and PQ = 5 cm
Let QR = x cm
∴PR = (25 – x)
∴By Pythagoras theorem, we have
PR2 = QR2 + PQ2
⇒(25 – x) = x2 + 52
⇒625 – 50x + x2 = x2 + 25
⇒–50x = –600
11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than,1.
(ii) 
for some valued of angle A.
for some valued of angle A. (iii) cos A is the abbreviation �used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v)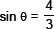 
for some angle q.
for some angle q.Sol. False [∵ A tangent of an angle is ratio of sides other than hupotenuse, which may be equal or unequal to each other.]
(ii) True ∵ cos A is always less than 1
(iii) False [∵ ‘cosine A’ is abbreviated as ‘cos A’
(iv) False [‘cot A’ is a single and meaningful term whereas ‘cot’ alone has no meaning.]
(v) False [∵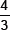 
is greater than 1 and sin B cannot be greater than 1.]
is greater than 1 and sin B cannot be greater than 1.]Exercise 8.2
1. Evaluate the following:
2. Choose the correct option and justify your choice:
(iii) When A = 0 then we have:
sin 2A = sin 2(0°) = sin 0° = 0
2 sin A = 2 sin 0 = 2 × 0 = 0
i.e., sin 2A = 2 sin A for A = 0°
Thus, the option (A) is correct
3. 
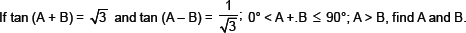
Sol. From the table, we have tan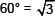 
...(1)
Also tan (A + B) =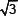 
(Given) ...(2)
From (1) and (2), we get
A + B = 60°
...(3)
Similarly,
A – B = 30°
...(4)
Adding (3) and (4),
2A = 90°.⇒ A = 45°
Subtracting (4) from (3), we get
2B = 30° ⇒ B = 15°.
4. State whether the following are true or false. Justify your answer.,
(i) sin (A + B) sin A + sin B.
(ii) The value of sinθ increases as θincreases.
(iii) The value of cosθ increases as θincreases.
(iv) sinθ= cosθ for all values of q.
(v) cot A is not defined for A = 0°.
Sol. (i) Let us take A = 30° and B = 60°
Then LHS = sin (30° + 60°)
= sin 90° = 1
RHS = sin 30° + sin 60°
Since, LHS ≠ RHS
∴ The statement sin (A + B) = sin A + sin B is false.
(ii) Since the values of sinθincreases from 0 to 1 as theθincreases from 0 to 90°.
∴ The given statement
(iii) Since the value of cosθecreases from1 to 0 asθincreases from 0 to 90°.
∴ The given statement is false.
(iv) Let us take 0 = 30°
⇒ sin 30° ≠ cos 30°
∴ The given statement .is false.
(iv) From the table, we have:
cot 0° = not defined.
∴ The given statement is true.
Exercise 8.3
1. Evaluate:
2. Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° � sin 38° sin 52° = 0
Sol. (i) tan 48° tan 23° tan 42° tan 67° =1
L.H.S. = tan 48° tan 23° tan 42° tan 67°
= tan (90° � 42°) tan 23° tan.42°.tan (90.° � 23°)
= cot 42° tan 23° tan 42° cot 23° [ tan (90 � A) = cot A]
= R.H.S.
Thus, tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52°
L.H.S. = cos 38° cos 52° – sin 52°
= cos 38° cos (90°– 38°)- sin 38° sin (90° – 38°)
= cos(38° sin 38° – sin 38° cos 38°
[∵sin (90° – A) = cos A and cos(90° – A) = sin A]
= 0 = R.H.S.
This, cos 38° cos 52° – sin 38° sin 52° = 0
3. If tan 2A cot (A �V 18�X), where 2A is an acute angle, find the value of A.
Sol. Since tan 2A = cot (A –18°)
Also tan (2A)° = cot (90° – 2A) [∵tan �� = cot (90° – θ)]
⇒ A – 18 = 90°– 2A
⇒ A + 2A = 90° + 18°
⇒ 3A = 108°
4. If tan A = cot B, prove that A + B = 90°.
Sol. tan A = cot B (given)
And cot B = tan (90° – B)
[∵tan (90° – θ ) = cot θ )]
∴ A = 90° – B
∴ A + B = 90°.
5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Sol. sec 4A = cosec (A – 20°)
sec (4A) = cosec (90° – 4A)
[∵cosec (90° – θ ) = sec θ )]
∴ A – 20° = 90° – 4A
⇒A + 4A = 90° + 20°
⇒ 5A = 110°
6. If A, B and C are interior angles of a triangle ABC, then show that
Sol. Since, sum of the angles of ΔABC is A° + B° + C° = 180°
∴ B + C = 180° – A
Dividing both sides by 2,
7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Sol. Since sin 67° = sin(90° – 23°)
= cos 23°
[∵sin (90° – θ ) = cos θ ]
Also, cos 75° = cos (90° – 15)
= sin 15°
[∵cos(90° – θ ) = sin θ ]]
∴ We have:
sin 67° + cos 75° = cos 23° + sin 15°.
Exercise 8.4
1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
2. Write all the other trigonometric ratios of ∠A in terms of sec A.
3. Evaluate:
(ii) sin 25° cos 65° + cos 25° sin 65°
sin 25° = sin (90° – 65) = cos 65°
[∵ sin (90° – A = cos A]
And cos 25° = cos (90° – 65°) = sin 65°
[∵ cos (90° – A = sin A]
∴ sin 25° cos 65° + cos 25° sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= (cos 65°)2 + (sin 65°)2
[∵ cos2 A + sin2 A = 1]
= cos2 65° + sin2 65°
= 1
4. Choose the correct option. Justify your choice.
(i) 9 sec2 A – 9 tan2 A = .................
(a) 1 (b) 9 (c) 8 (d) 0
(ii) (1 + tan θ + sec θ ) (1 + cot θ �n– cosec θ ) =
(a) 0 (b) 1 (c) 2 (d) –1
(iii) (sec A + tan A) (1 – sin A) = .................
(a) sec A (b) sin A (c) cosec A (d) cos A
Sol. (i) Since, 9 sec2 A – 9 tan2 A = 9 (sec2 A – tan2 A)
= 9 (1)
[∵tan2 A + 1 = sec2 A ⇒ sec2 A – tan2 A = 1]
= 9
∴ The option (b) is correct.
(ii) Here, (1 + tan θ + sec θ) (1 +cot ∵ – cosec θ)
5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(viii) (sin A + cosec A)2 + (cos A + sec A)2
= sin2 A + cosec2 A + 2 sin A . cosec A + cos2 A + sec2 A + 2 cos A . sec A
= (sin2 A + cos2 A) + cosec2 A + sec2 A + 2 + 2
[sin A . cosec A = 1 and sec A . cos A = 1]
= 1 + cosec2 A + sec2 A + 4
[∵sin2 A + cos2 A = 1]
= 5 + (1 + cot2 A) + (1 tan2 A)
[∵cosec2 A = 1 + cot2 A and sec2 A = 1 + tan2 A]
= 7 + cot2 A + tan2 A
= R.H.S.
(ix) L.H.S. = (cosec A – sin A) (sec A – cos A)
