Chapter 6: Application of Derivatives
Important Questions
1. Show that the function f(x) = x3 – 3x2 + 6x – 100 is increasing on
2. The volume of a sphere is increasing at the rate of 3 cubic centimeters per second. Find the rate of increase of its surface area, when the radius is 2 cm.
3. Show that the function f(x) = 4x3 – 18x2 + 27x – 7 is always increasing on R.
4. Sand is pouring from a pipe at the rate of 12 cm2/s. The falling and sand forms a cone on the ground in such a way the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
5. Find the intervals in which the function 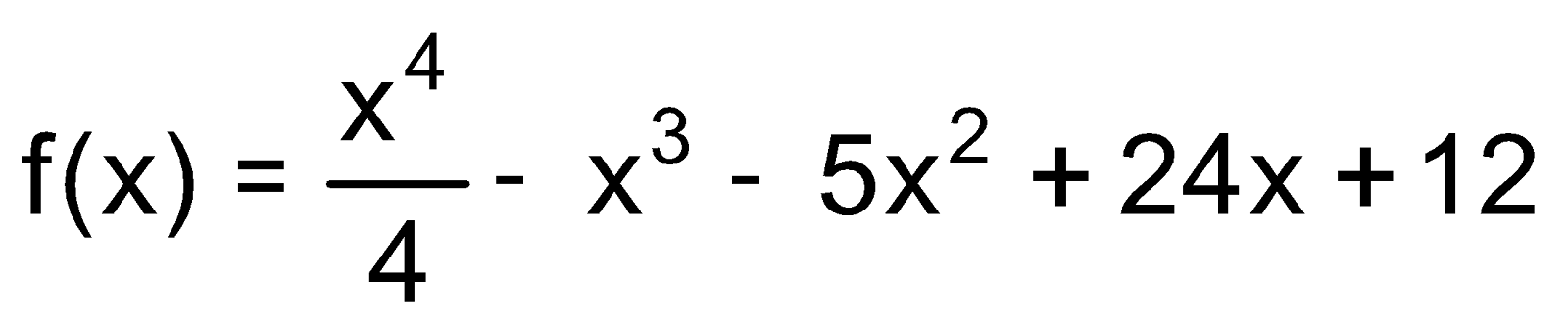 is
is
(a) Strictly increasing
(b) Strictly decreasing