Chapter 9: Differential Equations

1. Find the differential equation representing the curve y = cx + c².

2. Write the differential equations representing the family of curves y = mx, where m is an arbitrary constant.

3. Find the differential equation representing the family of curves 5 = ae^bx+5, where a and b are arbitrary constants.

4. Find the differential equation for all the straight lines, which are at a unit distance from the origin.

5. Prove that x² – y² = c(x² + y²)² is the general solution of the differential equation
(x³ – 3xy²)dx = (y³ – 3x²y)dy, where C is a parameter

1. Find the particular solution of the differential equation:
(1 – y²)(1+ logx)dx + 2xydy = 0 given that y = 0, when x = 1

2. Solve the following differential equation:

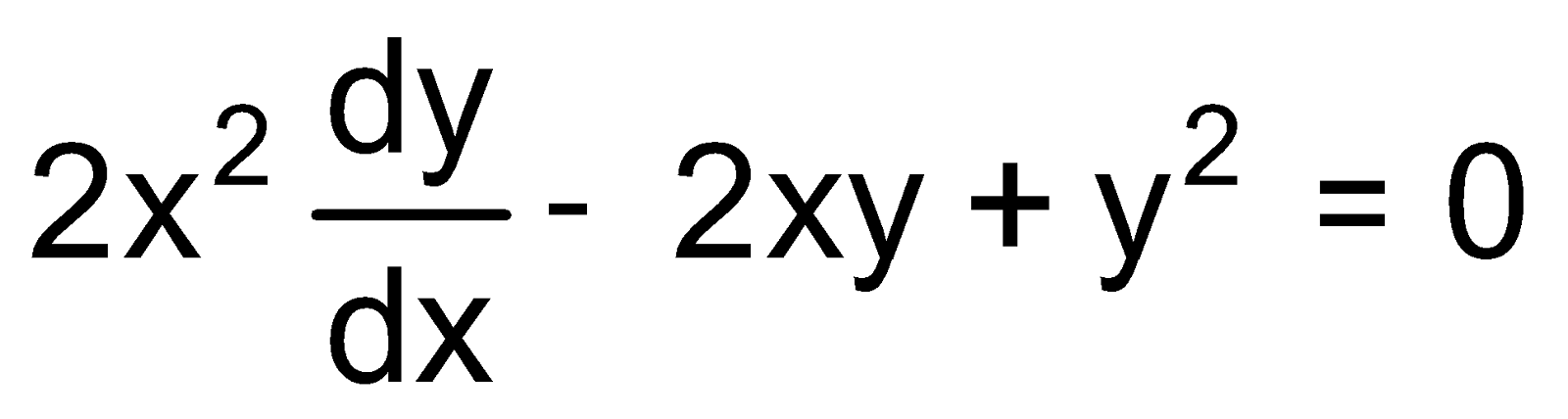
3. Find the particular solution of the following differential equation:
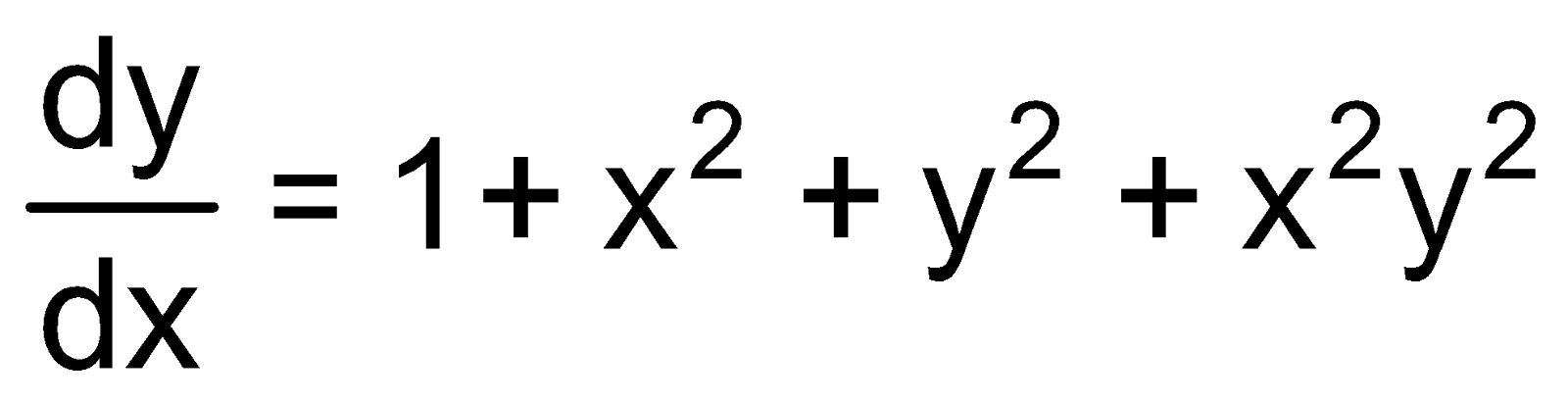, given that y = 1 when x = 0

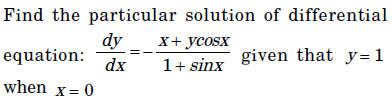
5. Solve the differential equation
(tan^–1 x – y)dx = (1 + x²)dy