Chapter 1: Relations and Functions
Important Questions
1. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
2. If the function f : R → R be defined by f(x) = 2x – 3 and g : R R by g(x) = x3 + 5, then find the value of (fog)–1 (x).
3. 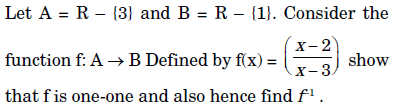
4. 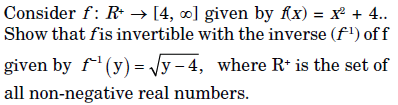
5. Let and A = R × R and * be a binary operation on A defined by (a,b) * (c,d) = (a + c,b + d). Show that * Find the identity element for * on A. Also find the inverse of every element (a, b) ∈ A.
Sample Questions
1. Let A = {x ∈ Z : 0 ≤ x ≤ 12}, Show {(a, b) : |a – b| is divisible by 4} that is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2].
2. Let * be a binary operation on N given by a * b = LCM (a, b) for all a,b ∈ N. Find 5*7.
3. If a*b denote the larger of ‘a' and ‘b' and if a O b =(a *b)+3 , then write the value of 5 O 10 , where * and O are binary operations.
4. Let A = Q × Q, where Q is the set of all rational numbers, and be a binary operation defined on A by (a, b) * (c, d) = (ac, b + ad), for all (a, b) (c, d) A. Find
(i) the identity element in A.
(ii) the invertible element of A.
5. Discuss the Commutativity and associativity of binary operation * defined on A = Q – {1} by the rule a * b = a – b + ab ∀a,b ∈ A . Also find the identity element of * in A and hence find the invertible elements of A.