Algebraic Expressions and Identities-NCERT Solutions

Class VIII Math
NCERT SOLUTIONS for ALGEBRAIC EXPRESSIONS
EXERCISE : 9.1
1.  Construct the following quadrilaterals:
      (i)   Quadrilateral ABCD
      (ii)  Quadrilateral JUMP
1.  Identify the terms, their coefficients for each of the following expressions:
      (i)   5xyz2 – 3zy
      (ii)  1 + x + x2
      (iii) 4x2y2 – 4x2y2z2 + z2
      (iv) 3 – pq + qr – rp
      (v)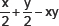
      (vi) 0.3 a – 0.6 ab + 0.5 b
Sol.  (i)     5xyz2 – 3zy
                    In the expression 5xyz2 – 3zy, the terms are 5xyz2 and –3zy.
                    coefficient of xyz2 in the term 5xyz2 is 5.
                    coefficient of zy in the term –3zy is –3.
          (ii)    1 + x + x2
                    In the expression 1 + x + x2, the terms are 1, x and x2.
                    Coefficient of x° in the term 1 is 1.
                    Coefficient of x in the term x is 1.
                    Coefficient of x2 is the term x2 is 1.
         (iii)    In the expression 4x2y2 – 4x2y2z2 + z2, the terms are 4x2y2, –4x2y2z2 and z2.
                    Coefficient of x2y2 in the term 4x2y2 is 4.
                    Coefficient of x2y2z2 in the term –4x2y2z2 is –4.
                    Coefficient of z2 in the term z2 is 1.
         (iv)    3 – pq + qr – rp
                    In the expression 3 – pq + qr – rp, the terms are 3, –pq, qr and –rp
                    Coefficient of x° in the term 3 is 3.
                    Coefficient pq in the term –pq is –1.
                    Coefficient qr in the term qr is 1.
                    Coefficient rp in the term –rp is 1.
          (v)    In the expression 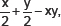the terms are
                    Coefficient of x in the term
                    Coefficient of y in the term
                    Coefficient of xy in the term – xy is – 1.
         (vi)    In the expression 0.3 a, – 0.6 ab and 0.5 b
                    Coefficient of a in the term 0.3a is 0.3.
                    Coefficient of ab in the term –0.6ab is
                    –0.6.
                    Coefficient of b in the term 0.5b is 0.5.
2.  Classify the following polynomials as monomials, bionomials, trinomlals. Which polynomials do not fit in any of these three categories?
      x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x,
      2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy,
      4z – 15z2,
      ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q.
Sol.  The given polynomials are classified as under:
          Monomials: 1000, pqr
          Binomials: x + y, 2y – 3y2, 4z – 15z2, p2q + pq2, 2p + 2q.
          Trinomials: 7 + y + 5x, 2y – 3y2 + 4y3,
          5x – 4y + 3xy.
          Polynomials that do not fit in any categories:
          x + x2 + x3 + x4, ab + bc + cd + da
3.  Add the following:
      (i) ab – bc, bc – ca, ca – ab
      (ii) a – b + ab, b – c + bc, c – a + ac
      (iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
      (iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
Sol.  (i)  Writing the given expressions in separate rows with like terms one below the other, we have
                  
           (ii) Writing the given expressions in separate rows with like terms one below the other, we have
                  
           (iii) Writing the given expressions in separate rows with like terms one below the other, we have
                  
           (iv) Writing the given expressions in separate rows with like terms one below the other, we have
                  
4.  (a) Subtract 4a – 7ab + 3b + 12
             from 12a – 9ab + 5b – 3
       (b) Subtract 3xy + 5yz – 7zx
             from 5xy – 2yz – 2zx + 10xyz
       (c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10
             from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q.
Sol.  Rearranging the terms of the given expressions, changing the sign of each term of the expression to be subtracted and adding the two expressions, we get.
          
          (b) Rearranging the terms of the given expressions, changing the sign of each term of the expression to be subtracted and adding the two expressions, we get.
               
          (c) Rearranging the terms of the given expressions, changing the sign of each term of the expression to be subtacted and adding the two expressions, we get.
               
EXERCISE : 9.2
1.  Find the product of the following pairs of monomials
       (i) 4, 7p                           (ii) – 4p, 7p
       (iii) – 4p, 7pq               (iv) 4p3, – 3p
       (v) 4p, 0
Sol.  (i)  4 × 7p = (4 × 7) × p = 28p
           (ii)  – 4p × 7p = (– 4 × 7) × (p × p)
                                       = 28 p1+1
                                       = 28p2q
           (iii)  –4p × 7pq = (–4 × 7) × (p × p × q)
                                          = – 28p1+1q
                                          = – 28p2q
           (iv)  4p3 × (–3p) = {4 × (–3)} × (p3 × p)
                                           = – 12 × p3+1
                                           = –12p4
           (v)  4p × 0 = (4 × 0) × (p)
                                = 0 × p
                                = 0.
2.  Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively:
      (p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2);
      (3mn, 4np)
Sol.  We know that the area of a rectangle = l × b, where l = length and b = breadth.
           Therefore, the areas of rectangles with pair of monomials (p, q); (10m, 5n); (20x2, 5y2);
           (4x, 3x2) and (3mn, 4np) as their lengths and breadths are given by
                  p × q = pq
                  10m × 5n = (10 × 5) × (m × n) = 50mn
                  20x2 × 5y2 = (20 × 5) × (x2 × y2)
                                        = 100x2y2
                  4x × 3x2 = (4 × 3) × (x × x2)
                                   = 12x3
                  and, 3mn × 4np = (3 × 4) × (m × n × n × p)
                                                   = 12mn2p
3.  Complete the table of products:
Sol.  Complete table is as under:
4.  Obtain the volume of rectangular boxes with the following length, breadth and height respectively:
      (i) 5a, 3a2, 7a4                              (ii) 2p, 4q, 8r
      (iii) xy, 2x2y, 2xy2                        (iv) a, 2b, 3c
Sol.  (i)  Required volume = 5a × 3a2 × 7a4
                    = (5 × 3 × 7) × (a × a2 × a4)
                    = 105a1+2+4 = 105a7
          (ii)  Required volume = 2p × 4q × 8r
                    = (2 × 4 × 8) × (p × q × r)
                    = 64 pqr.
          (iii)  Required volume = xy × 2x2y × 2xy2
                    = (1 × 2 × 2) × (xy × x2y × xy2)
                    = (4) × (x1+2+1 × y1+1+2)
                    = 4x4y4
          (iv)  Required volume = a × 2b × 3c
                    = (1 × 2 × 3) × (a × b × c)
                    = 6abc
5.  Obtain the product of
      (i) xy, yz, zx                        (ii) a, –a2, a3
      (iii) 2, 4y, 8y2, 16y3         (iv) a, 2b, 3c, 6abc
      (v) m, – mn, mnp
Sol.  (i)  xy × yz × zx = x × x × y × y × z × z
                                    = x1+1 xy1+1 × y1+1 × z1+1
                                    = x2y2z2
          (ii)  a × (–a2) × a3
                  = [1 × (–1) × 1] × (a × a × a × a × a × a)
                  = (–1) × (a6)
                  = –a6
          (iii)  2 × (4y) × 8y2 × 16y3
                  = (2 × 4 × 8 × 16) × (y × y2 × y3)
                  = (1024) × (y1 + 2 + 3)
                  = 1024y6
          (iv)  a × 2b × 3c × 6abc
                  = (2 × 3 × 6) × (a × b × c × abc)
                  = (36) × (a1+1 × b1+1 × c1+1)
                  = 36a2b2c2
          (v)  m × – mn × mnp
                  = (1 × – 1 × 1)× (m × m × m × n × n × p)
                  = –1 × m3 × n2 × p
                  = – m3n2p
EXERCISE : 9.3
1.  Carry out the multiplication of the expression in each of the following pairs:
      (i) 4p, q + r
      (ii) ab, a – b
      (iii) a + b, 7a2b2
      (iv) a2 – 9, 4a
Sol.  (i)  4p × (q + r)
                = 4p × q + 4p × r
                = 4pq + 4pr
          (ii)  ab × (a – b)
                ab × a – ab × (b)
                = a2b – ab2
          (iii)  (a + b) × (7a2b2)
                = 7a2b2 × a + 7a2b2 × b
                = 7a3b2 + 7a2b3
          (iv)  (a2
                – 9) × 4a
                = a2
                × 4a – 9 × 4a
                4a3 – 36a
          (v)  (pq + qr + rp) × 0 = 0
2.  Complete the table
       
Sol.  (i)  a(b + c + d)
                 = a × b + a × c + a × d
                 = ab + ac + ad
          (ii)  (x + y – 5) × (5xy)
                 = 5xy × x + 5xy × y + 5xy × (–5)
                 = 5x2y + 5xy2
                 – 25xy
          (iii)  6p3 – 7p2 + 5p
                  4p4q2 – 4p2q4
          (iv)  4p4q2 – 4p2q4
          (v)  a2bc + ab2c + abc2
3.  Find the product:
      (i) (a2) × (2a22) × (4a26)
      
      (iv) x × x2 × x3 × x4
Sol.  (i)  (a2) × (2a22) × (4a26)
                 = (1 × 2 × 4) × (a2 × a22 × a26)
                 = 8a2 + 22 + 26 = 8a50
          
4.  (a) Simplify : 3x(4x – 5) + 3 and find its value for
             
       (b) Simplify : a(a2 + a + 1) + 5 and find its                 value for (i) a = 0, (ii) a = 1, (iii) a = – 1
Sol.  (a) We have,
                  3x(4x – 5) + 3
                  = 3x × 4x – 3x × 5 + 3
                  = 12x2 – 15x + 3
          (i)    When x = 3, then
                  3x(4x – 5) + 3
                  = 3 × 3(4 × 3 – 5) + 3
                  = 12x2 – 15x + 3
                  = 9(12 – 5) + 3 = 9 × 7 + 3
                  = 63 + 3 = 66
          (ii)  When then 3x(4x – 5) + 3
                  
          (b)  We have,
                  a(a2 + a + 1) + 5
                  = a × a2 + a × a + a × 1 + 5
                  = a3 + a2 + a + 5
          (i)  a(a2 + a + 1) + 5
                  = 0(02 + 0 + 1) + 5
                  = 0(1) + 5
                  = 0 + 5 = 5.
          (ii)  When a = 1, then
                  a(a2 + a + 1) + 5
                  = (12 + 1 + 1) + 5
                  = 1(1 + 1 + 1) + 5
                  = 1(3) + 5 = 3 + 5 = 8.
          (iiI)  When a = –1, then
                  a(a2 + a + 1) + 5
                  = –1[(–1)2 + (–1) + 1] + 5
                  = –1(1 –1 + 1) + 5
                  = –1(1) + 5 = –1 + 5 = 4
5.  (a)  Add : p(p – q), q(q – r) and r(r – p)
       (b)  Add : 2x(z – x – y) and 2y(z – y – x)
       (c)  Subtract : 31(1 – 4m + 5n) from 41(10n – 3m + 21)
       (d)  Subtract : 3a(a + b + c) – 2b(a – b + c) from 4c(–a + b + c)
Sol.  (a)  p(p – q) + q(q – r) + r(r – p)
                  = p × p – p × q + q × q – q × r + r × r – r × p
                  = p2 – pq + q2 – qr + r2 – pr
                  = p2 + q2 + r2 – pq – qr – pr
          (b)  2x(z – z – y) + 2y(z – y – x)
                  = (2x × z) – (2x × x) – (2x × y)
                  + (2y × z) – (2y × y) – (2y × x)
                  = 2xz – 2x2 – 2xy + 2yz – 2y2 – 2xy
                  = – 2x2 – 2y2 – 4xy + 2xz + 2yz.
          (c)  4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
                  = (4l × 10n) – (4l × 3m) + (4l × 2l) + (–3l ×                                                            l) + (–3l × –4m) + (–3l × 5n)
                  = 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
                  = 5l2 + 25ln
          (d)  4c(–a + b + c) – {3a(a + b + c) – 2b(a – b + c)}
                  = {4c × (–a) + 4c × b + 4c × c}
                  –                            {(3a × a + 3a × b + 3a × c)} +
                         {(–2b × a) + (–2b × –b) + (–2b × c)}
                  = –4ac + 4bc + 4c2|
                  –{3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc}
                  = –4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac + 2ab – 2b2 + 2bc
                  = –3a2 – 2b2 + 4c2 – 7ac + 6bc – ab
EXERCISE : 9.4
1.  Multiply the binomials:
      (i) (2x + 5) and (4x – 3)
      (ii) (y – 8) and (3y – 4)
      (iii) (2.51 – 0.5m) and (2.51 + 0.5m)
      (iv) (a + 3b) and (x + 5)
      (v) (2pq + 3q2) and (3pq – 2q2)
      (vi)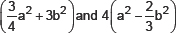
Sol.  (i)     (2x + 5) and (4x – 3)
                    = 2x(4x – 3) + 5(4x – 3)
                    = 8x2 – 6x + 20x – 15
          (ii)    (y – 8) × (3y – 4)
                    = y(3y – 4) –8(3y – 4)
                    = 3y2 – 4y – 24y + 3\2
                    = 3y2 – 28y + 32
          (iii)  (2.5l – 0.5m) × (2.5l + 0.5m)
                    = 2.5l(2.5l + 0.5m) – 0.5m(2.51 + 0.5m)
                    = 6.25l2 + 1.25lm – 1.25lm – 0.25m2
                    = 6.25l2 – 0.25m2
          (iv)   (a + 3b) × (x + 5)
                    = a(x + 5) + 3b(x + 5)
                    = ax + 5a + 3bx + 15b
                    = ax + 3bx + 5a + 15b
          (v)    (2pq + 3q2) × (3pq – 2q2)
                    = 2pq(3pq – 2q2) + 3q2(3pq – 2q2)
                    = 6p2q2 – 4pq3 + 9pq3 – 6q4
                    = 6p2q2
                    + 5pq3 – 6q4
          
2.  Find the product:
      (i) (5 � 2x)(3 + x)
      (ii) (x + 7y)(7x � y)
      (iii) (a2 + b)(a + b2)
      (iv) (p2 � q2)(2p + q)
Sol.  (i)     (5 � 2x)(3 +x)
                    = 5(3 + x) � 2x(3 + x)
                    = 15 + 5x � 6x � 2x2
                    = �2x2 � x + 15
          (ii)    (x + 7y)(7x � y)
                    = x(7x � y) + 7y(7x � y)
                    = 7x2 � xy + 49 xy � 7y2
                    = 7x2 + 48xy � 7y2
         (iii)    (a2 + b)(a +b2)
                    = a2(a +b2) + b(a + b2)
                    = a3 + a2b2 + ab + b3
         (iv)    (p2 � q2)(2p + q)
                    = p2(2p + q) � q2(2p + q)
                    = 2p3 + p2q � 2pq2 � q3
3.  Simplify:
      (i)   (x2 � 5)(x + 5) + 25
      (ii)  (a2 + 5)(b3 + 3) + 5
      (iii) (t + s2)(t2 � s)
      (iv) (a + b)(c � d) + (a � b)(c + d) + 2(ac + bd)
      (v) (x + y)(2x + y) + (x + 2y)(x � y)
      (vi) (x + y)(x2 xy + y2)
      (vii) (1.5x � 4y)(1.5x + 4y + 3) � 4.5x + 12y
      (viii) (a + b + c)(a + b � c)
Sol.  (i)     (x2 � 5)(x + 5) + 25
                    = x2(x + 5) � 5(x + 5) + 25
                    = x3 + 5x2 � 5x � 25 + 25
                    = x3 + 5x2 � 5x
          (ii)    (a2 + 5)(b3 + 3) + 5
                    = a2(b3 + 3) + 5(b3 + 3) + 5
                    = a2b2 + 3a2 + 5b3 + 15 + 5
                    = a2b3 + 3a2 + 5b3 + 20
         (iii)    (t + s2)(t2 � s)
                    = t(t2 � s) + s2(t2 � s)
                    = t3 � ts + s2t2 � s3
         (iv)    (a + b)(c � d) + (a � b)(c + d) + 2(ac + bd)
                    = a(c � d) + b(c � d) + a(c + d) � b(c + d) + 2ac + 2bd
                    = ac � ad + bc � bd + ac + ad � bc � bd                                                            + 2ac + 2bd
                    = 4ac
          (v)    (x + y)(2x + y) + (x + 2y)(x � y)
                    = x(2x + y) + y(2x + y) + x(x � y)                                                            + 2y(x � y)
                    = 2x2 + xy + 2xy + y2 + x2 � xy                                                            + 2xy � 2y2
                    = (2 + 1)x2 + (1 + 2 � 1 + 2)xy + (1 � 2)y2
                    = 3x2 + 4xy � y2
         (vi)    (x + y)(x2 � xy + y2)
                    = x(x2 � xy � y2) + y(x2 � xy + y2)
                    = x3 � x2y + xy2 + x2y � xy2 +y3
                    = x3 + y3
         (vii) (1.5x � 4y)(1.5x + 4y + 3) � 4.5x + 12y
                    = 1.5x(1.5x + 4y + 3) � 4y(1.5x + 4y + 3)                                             � 4.5x + 12y
                    = 1.5x � 1.5x + 1.5x � 4y + 1.5x � 3 � 4y                           � 1.5x � 4y � 4y � 4y � 3 � 4.5x + 12y
                    = 2.25x2 + 6xy + 4.5x � 6xy �16y2 � 12y                                                            � 4.5x + 12y
                    = 2.25x2 + (6 � 6)xy + (4.5 � 4.5)x � 16y2 + (�12 + 12)y
                    = 2.25x2 + (0)xy + (0)x � 16y2 + (0)y
                    = 2.25x2 + 0 + 0 � 16y2 + 0
                    = 2.25x2 � 16y2
         (viii) (a + b + c)(a + b � c)
                    = a(a + b � c) + b(a + b � c) + c(a + b � c)
                    = a2 + ab � ac + ab + b2 � bc + ac +                                                            bc � c2
                    = a2 + 2ab + b2 � c2
EXERCISE : 9.5
1.  Use a suitable identity to get each of the following products.
      (i)    (x + 3)(x + 3)
      (ii)  (2y + 5)(2y + 5)
      (iii) (2a – 7)(2a – 7)
      (iv)
      (v) (1.1m – 0.4)(1.1m + 0.4)
      (vi) (a2 + b2)(–a2 + b2)
      (vii) (6x – 7)(6x + 7)
      (viii) (–a + c)(–a + c)
      (ix)
      (x) (7a – 9b)(7a – 9b)
Sol.  (i)     (x + 3)(x + 3)
                    = x2 + (3 + 3)x + (3)(3)
                    [Using: (x + a)(x + b) = x2 + (a + b)x + ab]
                    = x2 + 6x + 9
                                        OR
                    (x +3)(x + 3) = (x + 3)2
                    = x2 + 2(3)x + (3)2|
                                        [Using: (a + b)2 = a2 + 2ab + b2]
                    = x2 + 6x + 9.
          (ii)    (2y + 5)2
                    = (2y)2 + 2(2y)(5) + (5)2
                                        {Using : (a + b)2 = a2 + 2ab + b2}
                    = 4y2 + 20y + 25.
         (iii)    (2a – 7)2
                    = (2a)2 – 2(2a)(7) + (7)2
                                        {Using : (a – b)2 = a2 – 2ab + b2}
                    = 4a2 – 28a + 49
         (iv)    
         (v)    (1.1m – 0.4)(1.1m + 0.4)
                    = (1.1m)2 – (0.4)2
                                        [Using: (a – b)(a + b) = a2 – b2]                                        = 1.21m2 – 16
         (vi) (a2 + b2)(– a2 + b2) = (b2 + a2)(b2 – a2)
                    = (b2)2 – (a2)2
                                        [Using: (a + b)(a – b) = a2 – b2]
                    = b4 – a4
         (vii) (6x – 7)(6x + 7) = (6x)2 – (7)2
                                        {Using: (a – b)(a + b) = a2 – b2}
                    = 36x2 – 49
         (viii) (–a + c)(–a +c)
                    = (–a + c)2 or (c – a)2
                    = (c)2 – 2(c)(a) + (a)2
                                        {Using: (a – b)2 = a2 – 2ab + b2}
                    = c2 – 2ac + a2
         (ix)
         (x) (7a – 9b)(7a – 9b) = (7a – 9b)2
                    = (7a)2 – 2(7a)(9b) + (9b)2
                                        {Using: (a – b)2 – 2ab + b2}
                    = 49a2 – 126ab + 81b2
2.  Use the identity (x + a)(x + b)
      = x2 + (a + b)x + ab to find the following products.
      (i)    (x + 3)(x + 7)
      (ii)  (4x + 5)(4x + 1)
      (iii) (4x – 5)(4x – 1)
      (iv) (4x + 5)(4x – 1)
      (v) (2x + 5y)(2x + 3y)
      (vi) (2a2 + 9)(2a2 + 5)
      (vii) (xyz – 4)(xyz – 2)
Sol.  (i)     (x + 3)(x + 7)
                    = x2 + (3 + 7)x + 3 × 7
                    = x2 + 10x + 21
          (ii)    (4x + 5)(4x + 1)
                    = (4x)2 + (5 + 1)4x + (5)(1)
                    = 16x2 + 24x + 5.
         (iii)    (4x – 5)(4x – 1)
                    = [4x + (– 5)][4x + (–1)]
                    = (4x)2 + [(–5) + (–1)]4x + (–5)(–1)
                    = 16x2 + (–5–1)4x + 5
                    = 16x2 – 24x + 5.
         (iv)    (4x + 5)(4x – 1)
                    = (4x + 5)(4x + (–1))
                    = (4x)2 + [5 + (–1)](4x) + (5)(–1)
                    = 16x2 + 16x – 5
         (v)    (2x + 5y(2x + 3y)
                    = (2x)2 + (5y + 3y)2x + (5y)(3y)
                    = 4x2 + (8y)(2x) + 15y2
                    = 4x2 + 16xy + 15y2
         (vi) (2a2 + 9)(2a2 + 5)
                    = (2a2)2 + (9 + 5)2a2 + (9)(5)
                    = 4a2 + 28a2 + 45
         (vii) (xyz – 4)(xyz – 2)
                    = (xyz)2 + (– 4 – 2)(xyz) + (–4)(–2)
                    = x2y2z2 – 6xyz + 8
3.  Find the following squares by using the identities:
      (i)    (b – 7)2
      (ii)  (xy + 3z)2
      (iii) (3x2 – 5y)2
      (iv)
      (v) (0.4p – 0.5q)2
      (vi) (2xy + 5y)2
Sol.  (i)     (b – 7)2
                    = b2 – 2(7)b + (7)2
                    = b2 – 14b + 49
          (ii)    (xy + 3z)2
                    = (xy)2 + 2(xy)(3z) + (3z)2
                                        {Using: (a + b)2 = a2 + 2ab + b2}
                    = x2y2 + 6xyz + 9z2
         (iii)    (3x2 – 5y)2
                    = (3x2)2 – 2(3x)2(5y) + (5y)2
                                        {Using: (a – b)2 = a2 – 2ab + b2}
                    = 9x4 – 30x2y + 25y2
         (iv)    
         (v) (0.4p � 0.5q)2
                    = (0.4p)2 � 2(0.4p)(0.5q) + (0.5q)2
                    = 0.16p2 � 0.4pq + 0.25q2
         (vi) (2xy + 5y)2
                    (2xy)2 + 2(2xy)(5y) + (5y)2
                                        [Using: (a + b)2 = a2 + 2ab + b2}
                    = 4x2y2 + 20xy2 + 25y2
4.  Simplify:
      (i)    (a2 � b2)2
      (ii)  (2x + 5)2 � (2x � 5)2
      (iii) (7m � 8n)2 + (7m + 8n)2
      (iv) (4m + 5n)2 + (5m + 4n)2
      (v) (2.5p � 1.5q)2 � (1.5p � 2.5q)2
      (vi) (ab + bc)2 � 2ab2c
      (vii) (m2 � n2m)2 + 2m3n2
Sol.  (i)     (a2 � b2)
                    = (a2)2 � 2(a2)(b2) + (b2)2
                                        [Using: (a � b)2 = a2 � 2ab + b2)
                    = a4 � 2a2b2 + b4
          (ii)    (2x + 5)2 � (2x � 5)2
                    {(2x)2 + 2(2x)(5) + (5)2} � {(2x)2 � 2(2x)(5) + (5)2}
                                        {Using: (a + b)2 = a2 + 2ab + b2 and (a � b)2 = a2 � 2ab + b2}
                    = (4x2 + 20x + 25) � (4x2 � 20x + 25)
                    = 4x2 + 20x + 25 � 4x2 + 20x � 25
                    = 40x
         (iii)    (7m � 8n)2 + (7m + 8n)2
                    = (49m2 � 112mn + 64n2)
                                        + (49m2 + 112mn + 64n2)
                    = 49m2 � 112mn + 64n2
                                        + 49m2 + 112m + 64n2
                    = 98m2 + 128n2
         (iv)    (4m + 5n)2 + (5m + 4n)2
                    = {(4m)2 + 2(4m)(5n) + (5n)2}
                                        +{(5m)2 + 2(5m)(4n) + (4n)2}
                    = 16m2 + 40mn + 25n2 + 25m2 + 40 mn + 16n2
                    = 16m2 + 25m2 + 25n2 + 80mn + 16n2
                    = 41m2 + 80mn + 41n2.
         (v)    (2.5p � 1.5q)2 � (1.5p � 2.5q)2
                    = (6.25p2 � 7.5pq + 2.25q2)
                                � (2.25p2 � 7.5pq + 6.25q2)
                    = (6.25 � 2.25)p2 + (�7.5 + 7.5)pq
                                        + (2.25 � 6.25)q2
                    = 4p2 + (0)pq � 4q = 4p2 � 4q2
         (vi) (ab + bc)2 � 2ab2c
                    = (ab)2 + 2(ab)(bc) + (bc2) � 2ab2c
                    = a2b2 + 2ab2c + b2c2 � 2ab2c
                    = a2b2 + b2c2
         (vii) (m2 – n2m)2 + 2m3n2
                    = {(m2)2 – 2(m2)(n2m) + (n2m)2} + 2m3n2
                    = m4 – 2m3n2 + m2n4 + 2m3n2
                    = m4 + m2 n4
5.  Show that:
      (i)    (3x + 7)2 – 84x = (3x – 7)2
      (ii)  (9p – 5q)2 + 180pq = (9p + 5q)2
      (iii)
      (iv) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
      (v) (a – b)(a + b) + (b – c)(b + c)
                              + (c – a)(c + a) = 0
Sol.  (i)     LHS = (3x + 7)2 – 84x
                    = (9x2 + 42x + 49) – 84x
                    = 9x2 – 42x + 49
                    = (3x)2 – 2(3x)(7) + (7)2
                    = (3x – 7)2 = RHS
          (ii)    LHS = (9p – 5q)2 + 180 pq
                    = {(9p)2 – 2(9p)(5q) + (5q)2} + 180 pq
                    = 81p2 – 90pq + 25p2 + 180 pq
                    = 81p2 + 90pq + 25q2
                    = (9p)2 + 2(9p)(5q0 + (5q)2
                    = (9p + 5q)2 = RHS.
         (iii)    
         (iv)    LHS = (4pq + 3q)2 � (4pq � 3q)2
                    = {(4pq)2 + 2(4pq)(3q) + (3q)2}
                                        � {(4pq)2 � 2(4pq)(3q) + (3q)2}
                    = {16p2q2 + 24pq2 + 9q2}
                                        � {16p2q2 � 24pq2 + 9q2}
                    = 16p2q2 + 24pq2 + 9q2 � 16p2q2
                                        + 24pq2 � 9q2
                    = 48pq2 = RHS
         (v) LHS = (a � b)(a + b) + (b � c)(b + c)
                                        + (c � a)(c + a)
                    = a2 � b2 + b2 � c2 + c2 � a2
                    = (a2 � a2) + (�b2 + b2) + (�c2 + c2)
                    = 0 + 0 + 0 = 0 = RHS
6.  Using identities, evaluate:
      (i)    712                        (ii) 992                        (iii) 1022
      (iv) 9982                        (v) 5.22                        (vi) 297 × 303                        (vii) 78 × 82 (viii) 8.92                        (ix) 1.05 × 9.5
Sol.  (i)     712
                    = (70 + 1)2 = (70)2 + 2 × 70 × 1 + (1)2
                                        {Using: (a + b)2 = a2 + 2ab + b2)
                    = 4900 + 140 + 1 = 5041
          (ii)    992
                    = (100 – 1)2
                    = (100)2 – 2 × 100 × 1 + (1)2
                                        [Using: (a – b)2 = a2 – 2ab + b2)
                    = 10000 – 200 + 1 = 9801
         (iii)    1022 = (100 + 2)2
                    = (100)2 + 2(100)(2) + (2)2
                                        [∵ (a – b)2 = a2 – 2ab + b2]
                    = 10000 + 4000 + 4 = 10404
         (iv)    9982
                    = (1000 – 2)3
                    = (1000)2 – 2(1000)(2) + (2)2
                                        [∵ (a – b)2 = a2 – 2ab + b2]
                    = 1000000 – 4000 + 4 = 996004
         (v) (5.2)2
                    = (5.0 + 0.2)2
                    = (5.0)2 + 2(5.0)(0.2) + (0.2)2
                                        [∵ (a + b)2 = a2 + 2ab + b2]
                    = 25 + 2 + 0.01 = 27.04
         (vi) 297 × 303
                    = (300 – 3) × (300 + 3)
                    = (300)2 – (3)2
                                        [Using: (a – b)(a + b) = a2 – b2]
                    = 90000 – 9 = 89991
         (vii) 78 × 82
                    = (80 – 2)(80 +2)
                    = (80)2 – (2)2
                                        [∵ (a + b)(a – b) = a2 – b2]
                    = 6400 – 4 = 6396
         (viii) 8.92
                    = (9 – 0.1)2
                    = (9)2 – 2(9)(0.1) + (0.1)2
                                        [Using: (a – b2) = (a2 – 2ab + b2]
                    = 81 – 1.8 + 0.01 = 79.21
         (ix) 1.05 × 9.5
                    = 1.05 × 0.95 × 10
                    = (1 + 0.05)(1 – 0.05) × 10
                    = [(1)2 – (0.05)2] × 10
                    = [1 – 0.0025] × 10
                                        [∵ (a + b)(a – b) = a2 – b2]
                    = 0.9975 × 10 = 9.975
7.  Using a2 � b2 = (a + b)(a � b)(a � b), find
      (i)    512 � 492
      (ii)  (1.02)2 � (0.98)2
      (iii) 1532 � 1472
      (iv) 12.12 � 7.92
Sol.  (i)     512 � 492
                    = (51 + 49) (51 � 49)
                    = (100)(2) = 200
          (ii)    (1.02)2 � (0.98)2
                    = (1.02 + 0.98)(1.02 � 0.98)
                    = (2)(0.04) = 0.08
         (iii)    1532 � 1472
                    = (153 + 147)(153 � 147)
                    = (300)(60) = 1800
         (iv)    12.12 � 7.92
                    = (12.1 + 7.9)(12.1 � 7.9)
                    = (20.0)(4.2) = 84
8.  Using (x + a)(x = b)
       = x2 + (a + b)x + ab, find
      (i)    103 � 104
      (ii)  5.1 � 5.2
      (iii) 103 � 98
      (iv) 9.7 � 9.8
Sol.  (i)     103 � 104
                    = (100 + 3)(100 + 4)
                    = (100)2 + (3 + 4)(100) + (3)(4)
                    = 10000 + 700 + 12 = 10712
          (ii)    5.1 � 5.2 = (5 + 0.1)(5 + 0.2)
                    = (5)2 + (0.1 + 0.2)(5) + (0.1)(0.2)
                    = 25 + 1.5 + 0.02 = 26.52
         (iii)    103 � 98 = (100 + 3)(100 � 2)
                    = (100)2 + [3 + (�2)](100) + (3)(�2)
                    = 10000 + 100 � 6
                    = 10094
         (iv)    9.7 � 9.8 = (10 � 0.3)(10 � 0.2)
                    = (10)2 + [(�0.3) + (�0.2)](10)
                                                                            + (�0.3)(�0.2)
                    = 100 + (�0.5)10 + 0.06 = 100.06 � 5
                    = 95.06