Mensuration-Notes

1 dm = 10 cm

1 dm³ or litre = 1 dm × 1 dm × 1 dm = (10 × 10 × 10) cm³ = 1000 cm³

1 cm = 10 mm

1m =100 cm

1m³ = (100 × 100 × 100) cm³ = 1000000 cm³

1 m³ = 1000 × 1000 cm³ = 1000 litre

1 kilolitre = 1m³ = 1000 litre

(mm) millimeter, ( cm) centimetre, (dm) decimetre, (m) metre

The geometrical figures which have only two dimensions are called as the plane figures.

A square with sides of 1 cm has an area of 1 cm².

Find the area of the shaded shape.

The shape covers 11 squares, so its area is 11 cm².

Find the area of the shaded triangle.

The triangle covers 6 full squares marked F, and 4 half squares marked H. Area = 6 + 2 = 8 cm².

Estimate the area of the shape shaded in the diagram.

This is a much more complicated problem as there are only 9 full squares marked F, but many other part square. You need to combine part squares that approximately make a whole square. For example, the squares marked make about 1 full square; the squares marked � make about 1 full square; the squares marked + make about 1 full square; the squares marked • make about 1 full square. Thus the total area is approximately

          9 + 4 = 13 cm².

(i)

Area of triangle

(ii) Area of an equilateral triangle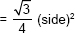

(iii) Area of an isosceles triangle :- base = b, equal side = a

        

The parallel sides of a trapezium are 20 cm and 10 cm. Its non-parallel sides are both equal, each being 13 cm. Find the area of the trapezium.

Let ABCD be a trapezium such that,

AB = 20 cm, CD = 10 cm and AD = BC = 13 cm

Draw CL || AD and CM || AB.

Now, CL || AD and CD || AB.

∴ ALCD is a parallogram.

⇒ AL = CD = 10 cm and CL = AD = 13 cm

In ΔCLB, we have CL = CB = 13 cm

∴ΔCLB is an isosceles triangle.

[∵BL= AB – AL = (20 – 10) cm = 10 cm]

Applying pythagoras theorem in δCML, we have

CL² = CM² + LM²

13² = CM² + 5²

CM² = 169 – 25 = 144

Area of parallelogram ALCD = AL × CM = (10 × 12) = 120 cm²

Hence, Area of trapezium ABCD = Area of parallelogram ALCD + Area of δCLB = (120 + 60) cm² = 180 cm²

If the area of a rhombus be 24 cm² and one of its diagonals be 4 cm, find the perimeter of the rhombus.

Let ABCD be a rhombus such that its one diagonal AC = 4 cm. Suppose the diagonals AC and BD intersect at O.

Area of rhombus ABCD = 24 cm²

Thus, we have AC = 4 cm and BD = 12 cm

Since the diagonals of a rhombus bisect each other at right angle. Therefore, δOAB is right triangle, right angled at 0.

Using pythagoras theorem in δOAB, we have

          AB² = OA² + OB²

          AB² = 22 + 62 = 40

          

Hence, perimeter of rhombus ABCD

Find the area of a regular octagon each of whose sides measures 4 cm.

Area of the octagon

The diagram shows a lorry.

Find the volume of the load-carrying part of the lorry.

The load-carrying part of the lorry is represented by a cuboid, so its volume is given by

V = 2 × 2.5 × 4 = 20m³.

A cuboid whose length, breadth and height are all equal is called a cube.

(i)   Surface area of a cube . Since alI the faces of a cube are squares of the same size i.e., for a cube we have l = b = h. Thus if l cm is the length of the edge of side of a cube, then

          Total Surface area of the cube = 2(l × l + l × l + l × l)

          = 2 × 3l² = 6l² = 6(Edge)²

(ii)  Lateral surface area of the cube = 2(l × l + l × l)

          = 2(l² + l²) = 4l² = 4(Fdge)²

(iii)  Volume of a cube = l × l × l = l³

Find the total surface of a hollow cylinder open at ends, if the length is 12 cm, the external diameter 10 cm and thickness 2 cm.

The outer radius (R) = 5 cm, Thickness = 2 cm

∴. Inner radius (r) = 5 cm – 2 cm = 3 cm

Outer curved surface of the cylinder

          = 2πrh = 2 × π × 5 × 12 = 120πcm²

Inner curved surface of the cylinder 27πrh

          = 2 × π × 3 × 12 = 72 π cm².

Both ends of the cylinder will be of the shape, as shown in figure (ii).

∴. Area of one of end of the cylinder = πR² – πr²

          = π × 5² – π × 3² = 25π – 9π = 16π cm².

Area of both ends = (2 × 16π) cm² = 32π cm²

∴Total surface of the cylinder = External curved surface + Internal curved surf ace + 2 (Area of the base of the ring)

          

Remark : It is advisible to put the value of π is the end in such calculations.

There are many objects around us which are conical in shape like an ice-cream cone, a conical, tent a birthday cap etc. These objects are of the shape of a right circular cone.

δAOC is right angled at O.

By Pythagoras theorem,

AC² = AO² + OC²

i.e. l² = h² + r²

(i)   Area of shaded region

          

(ii)  Total surface area of cone = Curved surface area of cone + Area of the circular base

          = πrl + πr²

          = πr (r + l) sq. units.

(iii) Volume of a cone 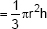(where ‘r’ r is the radius and ‘h’ is the height of cone).

Sphere: The set of all the points in space which are equidistant from a fixed point is called a sphere.

Hemisphere: A lane through the centre of a sphere divides the sphere into two equal parts and each part is called a hemisphere.

(i)   Curved surface area of hemisphere = 2πr²

(ii)  Total surface area of hemisphere 2πr² + πr² = 3πr²

If radius of the base of a cone is 140 dm and its slant height is 9 m. Find the

(i) curved surface area

(ii) total surface area

Radius of the base of the cone (r) = 140 dm = 14 m

Slant height (l) = 9 m

(i)   Curved surf ace area of the cone

(ii)  Total surface area of cone = πrl + πr²

          

The surface area of a sphere is 2464 dm². Find its diameter.

Surface area of a sphere = 2464 dm²

Therefore, 4πr² = 2464

                    

Diameter of the given sphere = 2 × 14 = 28 dm.

The dome of a building is in the form of a hemisphere of radius 63 dm.

Find the cost if it is to be painted at the rate of Rs 5 per m².

Radius of the hemisphere = 63 dm

Surface area of hemisphere = 2πr²

            

The earth taken out while digging a pit, is evenly sprea over a rectangular field of length 90 m, width 60 m.

If the volume of the earth dug is 3078 m3, find the height of the field raised.

3078 m³ = 90 m × 60m × h

height of field raised = 0.57 m