Practical Geometry-NCERT Solutions
Class VIII Math
NCERT Solutions For Practical Geometry
NCERT Solutions For Practical Geometry
EXERCISE : 4.1
1. Construct the following quadrilaterals:
(i) Quadrilateral ABCD
(ii) Quadrilateral JUMP
AB = 4.5 cm
JU = 3.5 cm
BC = 5.5 cm
UM = 4 cm
AD = 4 cm
MP = 5 cm
AD = 6 cm
PJ = 4.5 cm
AC = 7 cm
PU = 6.5
(iii) Parallelogram MORE
(iv) Rhombus BEST
OR = 6 cm
BE = 4.5 cm
RE = 4.5 cm
ET = 6 cm
EO = 7.5 cm
Sol. (i) First we draw a rough sketch of a quadrilateral ABCD and write down its dimensions as shown. We may divide it into two conveniently constructible Δs ABC and ACD.
Steps of construction:
1. Draw AC = 7 cm.
2. With A as centre and radius 4.5 cm, draw an arc (below AC).
3. With C as centre and radius 5.5 cm, draw another arc cutting the previous arc at B.
4. Join AB and BC
5. With A as centre and radius 6 cm, draw an arc (above AC).
6. With C as centre and radius 4 cm, draw another arc cutting the previous arc and D.
7. Join AD = CD.
Then, ABCD is the required quadrilateral.
(ii) First we draw a rough sketch of a quadrilateral JUMP and write down its dimensions as shown.
We may divide it inot two conveniently constructible Δs PJU and PMU.
Steps of construction:
1. Draw PU = 6.5 cm
2. With P as centre and radius 4.5 cm, draw an arc(below (PU)
3. With U as centre and radius 3.5 cm, draw another arc cutting the previous arc at J.
4. Join PJ and JU.
5. With P as centre and radius 5 cm, draw an arc (abov PU).
6. With U as centre and radius 4 cm, draw another arc cutting the previous arc at M.
7. Join PM and UM.
Then, JUMP is the required quadrilateral.
(iii) We know that opposite sides of parallelogram are equal and parallel to each other.
∴ OR = ME and MO = ER.
Steps of Construction:
1. Draw OR = 5 cm
2. With R as centre and radius equal to 4.5 cm, cut an arc.
3. With O as centre and radius equal to 7.5 cm, cut another arc on the arc drawn in step-2 at point E.
4. With E as centre and radius equal to 6 cm, cut an arc.
5. With O as centre and radius equal to 4.5 cm, cut an arc on the arc drawn in step-4 at point M.
6. Join RE, OE, OM and ME.
Hence, MORE is the required parallelogram.
(iv) We know that all four sides of a rhombus are equal.
∴ BE = ES = ST = BT = 4.5 cm.
Steps of Construction:
1. Draw BE = 4.5 cm.
2. With B as centre and radius equal to 4.5 cm, draw an arc.
3. With E as centre and radius equal to 6 cm, draw another arc, cutting the previous arc at point T.
4. With E as centre and radius equal to 4.5 cm, cut an arc.
5. With T as centre and radius equal to 4.5 cm, cut another arc on the previous arc at point S.
6. Join BT, ES, ET and ST.
Hence, BEST is the required rhombus.
EXERCISE : 4.2
1. Construct the following quadrilaterals:
(i) LI = 4 cm,
IF = 3 cm
TL = 2.5 cm,
LF = 4.5 cm
IT = 4 cm
(ii) Quadrilateal GOLD
OL = 7.5 cm,
GL = 6 cm
GD = 6 cm,
LD = 5 cm
OD = 10 cm
(iii) Rhombus BEND
BN = 5.6 cm,
DE = 6.5 cm
Sol. (i) Let us draw a rough sketch of the required quadrilateral and write down the dimensions. Clearly, the two easily constructible triangles are LIT and LIF.
Steps of construction:
1. Draw LI = 4 cm
2. With L as centre and radius 2.5 cm, draw an arc.
3. With I as centre and radius 4 cm draw another arc to cut the previous arc at T.
4. Join TL and TL
5. With L as centre and radius 4.5 cm, draw an arc.
6. With I as centre and radius 3 cm, draw another arc to cut the previously drawn arc at F.
7. Join FI, FL and TF.
Then, LIFT is the required quadrilateral.
(ii) Steps of construction:
1. Draw OL = 7.5 cm.
2. With L as centre and radius equal to 5 cm cut an arc.
3. With O as centre and radius equal to 10 cm, cut another arc on the arc drawn in step-2 at point D.
4. With L as centre and radius equal to 6 cm, cut another arc.
5. With D as centre and radius equal to 6 cm cut on arc drawn in step-4 at point G.
6. Join LD, LG, OG, OD and DG.
Hencem GOLD is the required quadrilateral.
Steps of construction:
1. Draw BN = 5.6 cm
2. Draw the right bisector XY of BN, meeting BN at O.
3. From O set off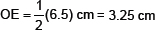 
along OY and OD = 3.25 cm along OX.
along OY and OD = 3.25 cm along OX. 4. Join BN, EN, ND and DB.
Then, BEND is the required rhombus.
EXERCISE : 4.3
1. Construct the following quadrilateral:
(i) Quadrilateral MORE
(ii) Quadrilateral PLAN
MO = 6 cm
PL = 4 cm
OR = 4.5 cm
LA = 6.5 cm
∠M = 60°
∠P = 90°
∠O = 105°
∠A = 110°
∠R = 105°
∠N = 85°
(iii) Parallelogram HEAR
(iv) Rectangle OKAY
HE = 5 cm
OK = 7 cm
EA = 6 cm
KA = 5 cm
∠R = 85°
Sol. (i) Draw a rough sketch of the required quadrilateral and write down its dimensions
Steps of construction:
1. Draw MO = 6 cm
2. Make ∠MOX = 105°
3. With O as centre and radius 4.5 cm, cut off OR = 4.5 cm long OX.
4. Make ∠ORY = 105°
5. Make ∠ZMO = 60° such that arms RY and MZ intersect at E.
Then, MORE is the required quadrilateral
Steps of construction:
1. Draw PL = 4 cm
2. Make ∠XPL = 90°
3. Make ∠YLP = 75°
4. With L as centre and radius 6.5 cm, cut off LA = 6.5 cm along LY.
5. Make ∠ZAL = 110° and let its arm AZ intersect PX at N.
Then, PLAN is the required quadrilateral.
(iii) Steps of construction:
1. Draw HE = 5 cm
2. Make ∠HEX = 85°
3. With A as centre and radius 5 cm draw an arc.
4. Join HR and AR.
Then HEAR is the required parallelgram.
(iv) Make a rough sketch of the required rectangle and write down its dimensions.
1. Draw OK = 7 cm
2. Draw ∠OKX = 90°
3. With K as centre and radius 5 cm, draw an arc KX at A.
4. With A as centre and radius 7 cm, draw an arc.
5. With O as centre and radius 5 cm, draw another arc cutting the previous arc at Y.
6. Join AY and OY.
Then, OKAY is the required rectangle.
EXERCISE : 4.4
1. Construct the following quadrilateals:
(i) Quadrilateral DEAR
(ii) Quadrilateral TRUE
DE = 4 cm
TR = 3.5 cm
ER = 5 cm
RU = 3 cm
AR = 4.5 cm
UE = 4 cm
∠E = 60°
∠R = 75°
∠A = 90°
∠U = 120°
Sol. Let us draw a rough sketch of the required quadrilateral and write down the given dimensions.
Steps of construction:
1. Draw EA = 5 cm
2. Make ∠XEA = 60°
3. With E as centre and radius 4 cm, cut off ED = 4 CM along EX.
4. Make ∠EAY = 90°
5. With A as centre and radius 4.5 cm, draw an arc to cut off AY at R.
6. Join DR.
Then, DEAR is the required quadrilateral.
(ii) Steps of Construction:
1. Draw RU = 3 cm.
2. Make ∠URX = 75° and ∠RUY = 120°
3. Cut off RT = 3.5 cm on RX and UE = cm on UY.
4. Join TE.
Hence, TRUE is the required quadrilateral.
EXERCISE : 4.5
Draw the following:
1. The square READ with RE = 5.1 cm.
Sol. Draw a rough sketch of the required square and write down its dimensions.
Steps of construction:
1. Draw RE = 5.1 cm
2. Draw RX ⊥ RE.
3. With R as centre and radius 5.1 cm, draw an arc to cut RX at D.
4. With D as centre and radius 5.1 cm, draw an arc.
5. With E as centre and radius 5.1 cm, draw another arc cutting the previous arc at A.
6. Join DA and EA.
Then READ is the required square.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
Sol. Let diagonal AC = 5.2 cm and diagonal BD = 6.4 cm
Draw AC = 5.2 cm. Draw XY, the perpendicular bisector of AC which cuts AC at O.
With O a centre, draw arcs of radii
which cut OX at D and OY at B.
Join AB, BC, CD and DA.
Then, ABCD is the required rhombus.
3. A rectangle with adjacent sides of lengths 5 cm and 4 cm.
Sol. In a rectangle, opposite sides are equal and each of 4 angles is equal to 90°.
Let AB = DC = 5 and BC = 4 cm
∴AB = DC = 5 cm and BC = AD = 4 cm.
Also, ∠A = ∠B = ∠C = ∠D = 90°.
Steps of construction
1. Draw AB = 5 cm.
2. Draw ∠ABX = 90°.
3. Cut off BC = 4 cm on BX.
4. With A as centre and radius equal to 4 cm, cut off an arc.
5. With C as centre and radius equal to 5 cm cut off another arc on the arc drawn in step-4 at point D.
6. Join AD and CD.
Hence, ABCD is the required rectangle.
4. A parallelgram OKAY where OK = 5.5 cm and KA = 4.2 cm.
Sol. In order to draw a quadrilateral, we need five measurements.
But here to draw the parallelogram OKAY, we are given two consecutive sides, i.e., four sides (the opposite sides being equal). So, we need information about one of its elements more. It may be the included angle between the sides or one of the diagonals to construct a unique quadrilateral. So, the required parallelogram cannot be drawn.