Constructions-NCERT Solutions

Q1.   Construct an angle of 90° at the initial point of a given ray and juste the construction.

Sol. Steps of construction:

        I. Draw a ray OA.

        II. Taking 0 as centre and suitable radius, draw a semicircle, which cuts OA at B.

        III. Keeping the radius same, divide the semicircle into three equal parts such that

        

        Thus, ∠AOF = 90°.

        Justification:

        ∵ O is the centre of the semicircle and it is divided into 3 equal parts.

        ∴∠BOC = ∠COD = ∠DOE

[∵Equal chords subtend equal angles at the centre]

        ∵∠BOC + ∠COD + ∠DOE = 180° ⇒ ∠BOC + ∠BOC + ∠BOC = 180°

        ⇒3∠BOC = 180°

        ∴ ∠BOC = 60°

        Similarly, ∠COD = 60° and ∠DOE = 60°

        ∵OF is the bisector of ∠COD.

        

Q2.   Construct an angle of 45� at the initial point of a given ray and juste the construction.

        Steps of construction:

        I. Draw a ray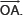

        II. Taking O as centre and with a suitable radius, draw a semicircle such that it intersects 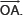at B.

        III. Taking Bas centre and keeping the same radius, cut the semicircle at C. Similarly cut the semicircle at D and E, such that Join OC and produce.

        IV. Divide B�lC into two equal parts, such that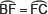

        V. Draw OG, the angle bisector of ∠FOC.

        Thus, ∠BOG = 45°

        or ∠AOG = 45°

        Justification:

        

Q3.   Construct the angles of the following measurements:

        

Solution: (i) Angle of 30°

        Steps of construction:

        I. Draw a ray OA.

        II. With 0 as centre and a suitable radius, draw an arc, cutting at B.

        III. With centre at B and the same radius as above, draw an arc to cut the previous arc at C.

        IV. Join and produce, such that ∠BOC = 60°.

        V. Draw bisector of ∠BOC, such that

        

        

        

Q4.   Construct the following angles and verb by measuring them by a protractor:

Sol. (i) Angle of 75°:

              Hint: 75° = 60° + 15°

        Steps of construction:

        I. Draw .

        II. With O as centre and having a suitable radius, draw an arc which meets at B.

        III. With centre B and keeping the radius same, mark a point C on the previous arc.'

        IV. With centre C and the same radius, mark another point D on the arc of step II.

        

        VI. Draw , the bisector of ∠COP, such that ∠COQ = 15°

             Thus, ∠BOQ = 60° + 15° = 75°

             or ∠AOQ = 75°.

        (ii) Angle of 105°:

             Hint: 105° = 90° + 15°

        Steps of construction:

        I . Draw .

        II. With centre 0 and having a suitable radius, draw an arc which meet OA at B.

        III. With centre B and keeping the same radius, mark a point C on the arc of step II.

        VI. With centre C and keeping the same radius, mark another point D on the arc of step II.

        V. Draw OP, the bisector of .

        VI. Draw OQ, the bisector of .

             Thus, ∠AOQ = 105°

        (iii) Angle of 135°:

             Hint: 120° + 15° = 135°

        Steps of construction:

        I. Draw a ray .

        II. With centre O and having a suitable radius draw an arc to meet OP at A.

        III. Keeping the same radius and starting from A, mark points Q, R and S on the arc of step II.

        VI. Draw 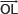, the bisector of .

        V. Draw OM, the bisector of .

             Thus, ∠POM = 135°.

Q5.   Construct an equilateral triangle, given its side and justify the construction.

Sol. Let us construct an equilateral triangle, each of whose side = PQ

             Steps of construction:

        I. Draw a ray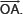

        II. Taking O as centre and radius equal to PQ, draw an arc to cut OA at B such that OB = PQ

        III. Taking B as centre and radius = OB, draw an arc, to intersect the previous arc at C.

        IV. Join OC and OB.

             Thus, ΔOBC is the required equilateral triangle.

             Justification:

             

Q1.   Construct a triangle ABC in which BC = 7 cm,

        ∠B = 75° and AB + AC = 13 cm.

Sol. Steps of construction:

        I. Draw a ray BX.

        II. From 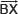, cut off = 7 cm.

        III. At B, construct ∠CBY = 75°.

        VI. From , cut off BD = 13 cm (= AB + BC)

        V. Join D and C.

        VI. Bisect DC such that the bisector of DC meets BD at A.

        VII. Join AC.

                Thus, ΔABC is the required triangle.

Q2.   Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.

Sol. Steps of construction:

        I. Draw a ray BX.

        II . From 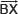, cut off = 8 cm.

        III. Construct ∠CBY = 45°.

        IV. From , cut off = 3.5 cm.

        V. Join D and C.

        VI. Draw PQ, perpendicular bisector of DC, which intersects at A.

        VII. Join AC.

              Thus, ABC is the required triangle.

Q3.   Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2cm.

Sol. Steps of construction:

        I . Draw a ray .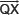

        II . From 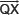, cut off QR = 6 cm.

        III. Construct a line YQY’ such that ∠RQY = 60°.

        IV. Cut off QS = 2 cm (from QY’).

        V. Join ‘S’ and ‘R’.

        VI. Draw MN, perpendicular bisector of SR, which intersects QY at P.

        VII.Join P and R.

                Thus, PQR is the required triangle.

Q4.   Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.

Sol. Steps of construction:

        I. Draw a line segment AB = 11 cm = (XY + YZ + ZX)

        II. Construct ∠BAP = 30° = ∠Y

        III. Construct ∠ABQ = 90° = ∠Z

        IV. Draw , the bisector of ∠BAP.

        V. Draw 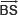, the bisector of ∠ABQ, such that and 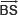intersect each other at X.

        VI. Draw perpendicular bisector of AX, which intersects AB at Y.

        VII.Draw perpendicular bisector of XB, which intersects AB at Z.

        VIII. Join XY and XZ.

                Thus, XYZ is the required triangle.

Q5.   Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.

Sol. Steps of construction:

        I. Draw = 12 cm.

        II. Construct ∠CBY = 90°.

        III. From , cut off BX = 18 cm.

        VI. Join CX.

        V. Draw PQ, the perpendicular bisector of CX, such that PQ meets BX at A.

        VI. Join AC.

                Thus, ABC is the required triangle.