Polynomials-NCERT Solutions

Class IX Math
NCERT Solutions For Polynomials
Exercise– 2.1
1.  Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
Ans. (i)   4x2 – 3x + 7
                ⇒ 4x2 – 3x + 7x°
                ∵ All the exponents of x are whole numbers.
                ∴ 4x2 – 3x + 7 is a polynomial in one variable.
         (ii)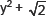   
                 
                ∵ All the exponents of y are whole numbers.
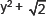                ∴ is a polynomial in one variable.
         
         
         (v)   x10 + y3 + t50
                ∵; Exponent of every variable is a whole number,
                ∴ x10 + y3 + t50 is a polynomial in x, y and t, i.e. in three variables.
2.  Write the co-efficients of x2 in each of the following:
         (i)   2 + x2 + x
         (ii)   2 – x2 + x3
         (iii)   
         (v)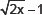   
Ans. (i)   2 + x2 + x
                The co-efficient of x2 is 1.
         (ii)   2 – x2 + x3
                The co-efficient of x2 is (–1).
         (iii)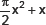   
                The co-efficient of x2 is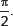
         (iv)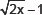   
                
                ∴  The co-efficient of x2 is 0
3.  Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Ans. (i)   A binomial of degree 35 can be: 3x35 – 4
         (ii)   A monomial of degree 100 can be: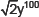
4.  Write the degree of each of the following polynomials:
         (i)   5x3 + 4x2 + 7x
         (ii)   4 - y2
         (iii)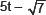   
         (iv)   3
Ans. (i)   5x3 + 4x2 + 7x
                ∵ The highest exponent of x is 3.
                ∴ The degree of the polynomial is 3.
         (ii)   4 – y2
                ∵ The highest exponent of y is 2.
                ∴ The degree of the polynomial is 2.
         (iii)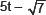   
                ∵ The highest exponent of t is 1.
                ∴ The degree of the polynomial is 1.
         (iv)   3
                since, 3 = 3x°
                ∴ The degree of the polynomial 3 is 0.
5.  Classify the following as linear, quadratic and cubic polynomials:
         (i)   x2 + x
         (ii)   x – x3
         (iii)   y + y2 + 4
         (iv)   1 + x
         (v)   3t
         (vi)   r2
         (vii)   7x3
Ans. (i)   x2 +x
                ∵ The degree of x2 + x is 2.
                ∴ It is a quadratic polynomial.
         (ii)   x – x3
                ∵ The degree of x – x3 is 3.
                ∴ It is a cubic polynomial.
         (iii)   y + y2 + 4
                ∵ The degree of y + y2 + 4 is 2.
                ∴ It is a quadratic polynomial.
         (iv)   1 + x
                ∵ The degree of 1 + x is 1.
                ∴ It is a linear polynomial.
         (v)   3t
                ∵ The degree of 3t is 1.
                ∴ It is a linear polynomial.
         (vi)   r2
                ∵ The degree of r2 is 2.
                ∴ It is a quadratic polynomial.
         (vii)   7x3
                ∵ The degree of 7x3 is 3.
                ∴ It is a cubic polynomial.
Exercise– 2.2
1.  Find the value of the polynomial 5x – 4x2 + 3 at
         (i)   x = 0
         (ii)   x = –1
         (iii)   x = 2
Ans. (i)   ∵ p(x) = 5x – 4x2 + 3 = 5(x) – 4(x)2 + 3
                  ∴ p(0) = 5(0) – 4(0) + 3 = 0 – 0 + 3 = 3
                  Thus, the value of 5x – 4x2 + 3 at x = 0 is 3.
         (ii)   ∵ p(x) = 5x – 4x2 + 3 = 5(x) – 4(x)2 + 3
                 ∴ p(–1) = 5(–1) – 4(–1)2 + 3 = – 5 – 4(1) + 3
                 = –5 – 4 + 3 = –9 + 3 = –6
                 ∴ The value of 5x – 4x2 + 3 at x = –1 is –6.
         (iii)  ∵ p(x) = 5x – 4x2 + 3 = 5(x) – 4(x)2 + 3
                 ∴ p(2) = 5(2) – 4(2)2 + 3 = –10 – 4(4) + 3
                 = 10 – 16 + 3 = –3
                 Thus the value of 5x – 4x2 + 3 at x = 2 is –3
2.  Find p(0), p(1) and p(2) for each of the following polynomials:
         (i)     p(y) = y2 – y + 1
         (ii)    p(t) = 2 + t + 2t2 – t3
         (iii)   p(x) = x3
         (iv)   p(x) = (x – 1) (x + 1)
Ans. (i)   p(y) = y2 – y + 1
                  ∵ p(y) = y2 – y + 1 = (y)2 – y + 1
                  ∴ p(0) = (0)2 – (0) + 1 = 0 – 0 + 1 = 1
                  p(1) = (1)2 – (1) + 1 = 1 – 1 + 1 = 1
                  p(2) = (2)2 – 2 + 1 = 4 – 2 + 1 = 3
         (ii)   p(t) = 2 + t + 2t2 – t3
                ∵ p(t) = 2 + t + 2t2 – t3 = 2 + t + 2(t)2 – (t)3
                ∴ p(0) = 2 + (0) + 2(0)2 – (0)3
                = 2 + 0 + 0 – 0 = 2
                p(1) = 2 + (1) + 2(1)2 – (1)3
                = 2 + 1 + 2 – 1 = 4
                p(2) = 2 + 2 + 2(2)2 – (2)3 = 2 + 2 + 8 – 8 = 4              (iii)   p(x) = x3
                ∵ p(x) = x3 = (x)3
                ∴ p(0) = (0)3 = 0
                p(1) = (1)3 = 1
                p(2) = (2)3 = 8                [∵ 2 × 2 × 2 = 8]
         (iv)   p(x)= (x – 1)(x + 1)
                ∵ p(x) = (x – 1)(x + 1)
                ∴ p(0) = (0 – 1)(0 + 1) = –1 × 1 = –1
                p(1) = (1 – 1)(1 + 1) = (0)(2) = 0
                p(2) = (2 – 1)(2 + 1) = (1)(2) = 3
3.  Verify whether the following are zeros of the polynomial, indicated against them.
       
Ans. (i)   ∵ p(x) = 3x + 1
       
         (iii)   Since, p(x) = x2 – 1
                ∴ p(1) = (1)2 – 1 = 1 – 1 = 0
                Since, p(1) = 0,
                ∴ x = 1 is a zero of x2 – 1.
                Also p(–1) = (–1)2 – 1 = 1 – 1 = 0
                i.e. p(–1) = 0,
                ∴ x = –1 is also a zero of x2 – 1.
         (iv)   We have p(x) = (x + 1)(x – 2)
                ∴ p(–1) = (–1 + 1)(–1 – 2) = (0)(–3) = 0
                Since p(–1) = 0,
                ∴ x = –1 is a zero of (x + 1)(x – 1).
                ∴ Also, p(2) = (2 + 1)(2 – 2) = (3)(0) = 0
                ∴ Since p(2) = 0,
                ∴ x = 2 is also a zero of (x + 1)(x – 1).
         (v)   We have p(x) = x2
                ∴ p(0) = (0)2 = 0
                Since p(0) = 0,
                ∴ 0 is a zero of x2.
         (vi)   We have p(x) = lx + m
                   
         (vii)   We have p(x) = 3x2 – 1
                   
         (viii)   We have p(x) = 2x + 1
                   
                    is not a zero of 2x + 1.
4.  Find the zero of the polynomial in each of the following cases:
         (i)   p(x) = x + 5
         (ii)   p(x) = x – 5
         (iii)   p(x) = 2x + 5
         (iv)   p(x) = 3x – 2
         (v)   p(x) = 3x
         (vi)   p(x) = ax, a ≠ 0
         (vii)   p(x) = cx + d, c ≠ 0, c, d are real numbers.
Ans. (i)   We have p(x) = x + 5
                ∴ p(x) = 0
                ⇒ x + 5 = 0
                ∴ or x = –5
                ∴ Thus, a zero of x + 5 is (–5).
         (ii)   We have p(x) = x – 5
                ∴ p(x) = 0
                ⇒ x – 5 = 0
                ∴ or x = 5
                ∴ Thus, a zero of x – 5 is 5.
         (iii)   We have p(x) = 2x + 5
                ∴ p(x) = 0
                ⇒ 2x + 5 = 0
                or 2x = –5
                
                

Thus, a zero of 3x – 2 is
         (v)   Since p(x) = 3x
                ∴ p(x) = 0
                ⇒ 3x = 0
                
                Thus, a zero of 3x is 0.
         (vi)   Since, p(x) = ax, a ≠ 0
                ∴ p(x) = 0
                ⇒ ax = 0
                or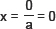
                Thus, a zero of ax is 0.
         (viii)   Since, p(x) = cx + d
                ∴ p(x) = 0
                ⇒ cx + d = 0
                 or cx = –d
                or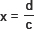
                Thus, a zero of cx + d is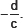
5.  If p(x) = x2 – 4x + 3, evaluate: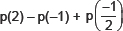
Ans. We have p(x) = x2 4x + 3
                ∴ p(–1) = (–1)2 – 4(–1) + 3
                = 1 + 4 + 3 = 8
                and p(2) = (2)2 – 4(2) + 3
                = 4 – 8 + 3 = –1
                 
Exercise– 2.3
1.  Find the remainder when x3 + 3x2 + 3x + 1 is divided by
         (i)   x + 1
         (ii)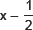   
         (iii)   x
         (iv)   x + π
         (v)   5 + 2x
Ans. (i)   ∴ The zero of x + 1 is –1
                And by remainder theorem, when
                p(x) = x3 + 3x2 + 3x + 1 is divided by x + 1, then remainder is p(–1).
                ∴ p(–1) = (–1)3 + 3 (–1)2 + 3(–1) + 1
                = –1 + (3 × 1) + (–3) + 1
                = –1 + 3 – 3 + 1
                = 0
                Thus, the required = 0
                
                and p(x) = x3 + 3x2 + 3x + 1
                ∴ For divisor 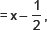remainder is given as
                
         (iii)   We have p(x) = x3 + 3x2 + 3x + 1 and the zero of x is 0
                p(0) = (0)3 + 3(0)2 + 3(0) + 1
                = 0 + 0 + 0 +1 = 1
                Thus, the required remainder = 1.
         (iv)   We have p(x) = x3 + 3x2 + 3x + 1 and zero of x + p = (–p)
                [∵ x + π = 0 ⇒ x = –π]
                ∴ p(–π) = (–5)3 + 3(–π)2 + 3(–π) + 1
                = –π3 + 3(π2) + (–3π) + 1
                = –π3 + 3π2 – 3π + 1
                Thus, the required remainder is –π3 + 3π2 – 3π + 1.
         (v)   We have (p(x) = x3 + 3x2 + 3x + 1 and zero of 5 + 2x is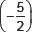
                 
2.  Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Ans. We have p(x) = x3 – ax2 + 6x – a
                ∵ Zero of x – a is a.
                [∵ x – a = 0 ⇒ x = a]
                ∴ p(a) = (a)3 a(a)2 + 6(a) – a = a3 – a3 + 6a – a
                = 0 + 5a = 5a
                ∴ Thus, the required remainder = 5a
3.  Check whether 7 + 3x is a factor of 3x3 + 7x.
Ans. We have p(x) = 3x3 + 7x and zero of 7 + 3x is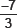
                 
                i.e. the remainder is not 0.
                ∴ 3x3 – 7x is not divisible by 7 + 3x.
                Thus, (7 + 3x) is not a factor of 3x3 – 7x.
Exercise– 2.4
1.  Determine which of the following polynomials has a factor (x + 1):
         (i)   x3 + x2 + x + 1
         (ii)   x4 + x + x2 + x + 1
         (iii)   x4 + 3x3 + 3x2 + x +1
         (iv)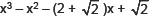   
Ans. For x + 1 = 0, we have x = –1.
         (i)   p(x) = x3 + x2 + x + 1
                ∴ p(–1) = (–1)3 + (–1)2 + (–1) + 1
                = –1 + 1 – 1 + 1 = 0
                i.e. when p(x) is divided by (x + 1), then the remainder is zero.
                ∴ (x + 1) is a factor of x3 + x2 + x + 1.
         (ii)   p(x) = x4 + x3 + x2 +x + 1
                ∴ p(–1) = (–1)4 + (–1)3 + (–1)2 + (–1) + 1
                = 1 – 1 + 1 – 1 + 1
                = 3 – 2 = 1
                ∵ p(x) is not divisible by x + 1.
                i.e. (x + 1) is not a factor of
                x4 + x3 + x2 + x + 1.
         (iii)  ∵ p(x) = x4 + x3 + x2 +x + 1
                ∴ p(–1) = (–1)4 + 3(–1)3 + 3(–1)2 + (–1) + 1
                = (1) + 3(– 1) + 3(1) + (– 1) + 1
                = 1 – 3 + 3 – 1 + 1
                = 1 ≠ 0
                ∵ f(–1) ≠ 0
                ∴ (x + 1) is not a factor of x4 + 3x3 + 3x2 +x +1.
         
2.  Use the factor theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
         (i)   p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
         (ii)   p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
         (iii)   p(x) = x3 – 4x2 + x + 6, g(x) = x – 3
Ans. (i)   We have p(x) = 2x3 + x2 – 2x – 1 and g(x) = x + 1
                ∴ p(–1) = 2(–1)3 + (–1)2 – 2(–1) – 1
                = 2(–1)3 + (–1)2 – 2(–1) – 1
                = 2(–1) + 1 + 2 – 1
                = –2 + 1 + 2 – 1
                = –3 + 3 = 0
                ∵ p(–1) = 0
                ∴ g(x) is a factor of p(x).
         (ii)   We have p(x) = x3 + 3x2 + 3x + 1 and g(x) = x + 2
                ∴ p(–2) = (–2)3 + 3(–2)2 + 3(–2) + 1
                = –8 + 3(4) + (–6) + 1
                = –8 + 12 – 6 + 1
                = –8 – 6 + 12 + 1
                = –14 + 13 = –1
                ∵ p(–2) ≠ 0
                Thus, g(x) is not a facot of p(x).
         (iii)   We have p(x) = x3 – 4x2 + x + 6 and g(x) = x – 3
                ∴ p(3) = (3)3 – 4(3)2 + (3) + 6
                = 27– 4(9) + 3 + 6
                = 27– 36 + 3 + 6 = 0
                Since g(x) = 0
                ∴ g(x) is a factor of p(x).
3.  Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
                 
Ans. Here p(x) = x3 + x + k
                For x – 1 be a factor of p(x), p(1) should be equal to 0.
                We have p(1) = (1)3 + 1 + k
                or p(1) = 1 + 1 + k = k + 2
                ∴ k + 2 = 0
                ⇒ k = –2
         (ii)   Here, p(x) = 2x2 + kx + 2
                For x – 1, be a factor of p(x), p(1) = 0
                Since,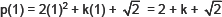
                ∵ p(1) must be equal to 0.
                ⇒ k = –2 – 2
                or k = –(2 + 2 ).
         (iii)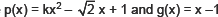   
                ∴ For (x – 1) be a factor of p(x), p(1) should be equal to 0.
                
         (iv)   Here p(x) = kx2 – 3x + k and g(x) = x – 1
                For g(x) be a factor of p(x), p(1) should be equal to 0.
                Since p(1) = k(1)2 – 3(1) + k
                = k – 3 + k
                = 2k – 3
                ∴ 2k – 3 = 0
                
4.  Factorise:
         (i)   12x2 – 7x + 1
         (ii)   2x2 + 7x + 3
         (iii)   6x2 + 5x – 6
         (iv)   3x2 – x – 4
Ans. (i)   12x2 – 7x + 1
                Here co-efficient of x2 = 12
                Co-efficient of x = –7
                and constant term = 1
                ∴ a = 12, b = –7, c = 1
                Now, l + m = –7 and lm = ac = 12 × 1
                ∴ We have l = (–4) and m = (–3)
                i.e. b = –7 + (–4 –3).
                Now, 12x2 –7x + 1 = 12x2 – 4x – 3x + 1
                = 4x(3x – 1) – 1(3x – 1)
                = (3x – 1)(3x – 1)
                Thus, 12x2 – 7x + 1 = (3x – 1)(3x – 1)
         (ii)   2x2 + 7x + 3
                Here, a = 12, b = –7, c = 1
                ∴ l + m = 7 and lm = 2 × 3 = 6
                i.e. l + 6 = 7 and 1 × 6 = 6∴ l = 1 and m = 6
                We have
                2x2 + 7x + 3 = 2x2 + x + 6x + 3
                = x(2x + 1) + 3(2x + 1)
                = (2x + 1)(x + 1)
                Thus, 2x2 + 7x + 3 = (2x + 1)(x + 1)
         (iii)   6x2 + 5x – 6
                We have a = 6, b = 5 and c = –6
                ∴ l + m = 5 and lm = ac = 6 × (–6) = –36
                ∴ l + m = 9 + (–4)
                ∴ 6x2 + 5x – 6 = 6x2 + 9x – 4x – 6
                = 3x(2x + 3) – 2(2x + 3)
                = (2x + 3)(3x – 2)
                Thus, 6x2 + 5x – 6 = (2x + 3)(3x – 2)
         (iv)   3x2 – x – 4
                We have a = 3, b = –1 and c = –4
                ∴ l + m = –1 and lm = 3 × (–4) = –12
                ∴ l = – 4 and m = 3
                Now, 3x2 – x – 4 = 3x2 – 4x + 3x – 4
                = x(3x – 4) + 1(3x – 4)
                = (3x – 4)(x + 1)
                Thus, 3x2 – x – 4 = (3x – 4)(x + 1)
5.  Factorise:
         (i)   x3 – 2x2 – x + 2
         (ii)   x3 – 3x2 – 9x – 5
         (iii)   x3 + 13x2 + 32x + 20
         (iv)   2y3 + y2 – 2y – 1
Ans. (i)   x3 – 2x2 – x + 2
                Rearranging the terms, we have
                x3 – 2x2 – x + 2 = x3 – x – 2x2 + 2
                = x(x2 – 1) – 2(x2 – 1)
                = (x2 – 1) (x – 2)
                = [(x2 – (1)2][x – 2]
                = (x – 1) (x + 1)(x – 2)
                [∴ a2 – b2 = (a + b)(a – b)]
                Thus,
                x3 – 2x2 – x + 2 = (x – 1) (x + 1)(x – 2)
         (ii)   x3 – 3x2 – 9x – 5
                We have p(x) = x3 – 3x2 – 9x – 5
                By trial, let us find:
                p(1) = (1)3 – 3(1)2 – 9(1) –5
                = 3 – 3 – 9 – 5
                = –14 ≠ 0
                Now p(–1) = (–1)3 – 3(–1)2 – 9(–1) –5
                = –1 – 3(1) + 9 – 5
                = –1 – 3 + 9 – 5 = 0
                ∴ By factor theorem, [x – (–1)] is a factor of p(x).
                Now,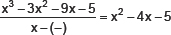
                ∴ x3 – 3x2 – 9x – 5 = (x + 1)(x2 – 4x – 5)
                = (x + 1)[x2 – 5x + x – 5]
                [Splitting –4 into –5 and +1]
                = (x + 1)[x(x – 5) +1(x – 5]
                = (x + 1)[(x – 5) (x + 1)]
                = (x + 1)(x – 5)(x + 1)
         (iii)   x3 + 13x2 + 32x + 20
                We have p(x) = x3 + 13x2 + 32x + 20
                By trial, let us find:
                p(1) = (1)3 + 13(1)2 + 32(1) + 20
                = 1 + 13 + 32 + 20
                = 66 ≠ 0
                Now
                p(–1) = (–1)3 + 13(–1)2 + 32(–1) + 20
                = –1 + 13 – 32 + 20
                = 0
                ∴ By factor theorem, [x – (–1)], i.e. (x + 1) is a factor p(x).
                
                or x3 + 13x2 + 32x + 20
                = (x + 1) (x2 + 12x + 20)
                = (x + 1) (x2 + 2x + 12x + 20)
                [Splitting the middle term]
                = (x + 1)[x(x + 2) + 10(x + 2)]
                = (x + 1)[(x + 2) (x + 10)]
                = (x + 1)(x + 2) (x + 10)
         (iv)   2y3 + y2 – 2y – 1
                We have p(y) = 2y3 + y2 – 2y – 1
                By trial, we have
                p(1) = 2(1)3 + (1)2 – 2(1) – 1
                = 2(1) + 1 – 2 – 1
                = 2 + 1 – 2 – 1 = 0
                ∴ By factor theorem, (y – 1) is a factor of p(y).
                
                ∴ 2y3 – y2 – 2y – 1 = (y – 1)(2y2 + 3y + 1)
                = (y – 1)[2y2 + 2y + y + 1)
                [Splitting the middle term]
                = (y – 1)[2y(y + 1) + 1(y + 1)]
                = (y – 1)[(y + 1) (2y + 1)]
                = (y – 1)(y + 1) (2y + 1)
Exercise– 2.5
1.  Use suitable identities to find the following products:
         (i)   (x + 4) (x + 10)
         (ii)   (x + 8) (x – 10)
         (iii)   (3x + 4)(3x – 5)
         (iv)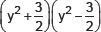   
         (v)   (3 – 2x) (3 + 2x)
Ans. (i)   (x + 4) (x + 10):
                   Using the identity
                (x + a)(x + b) = x2 + (a + b)x + ab, we have:
                (x + 4)(x + 10) = x2 + (14 + 10)x + (4 × 10)
                = x2 + 14x + 40
         (ii)   (x + 8) (x – 10):
                Here, a = 8 and b = (–10)
                ∴ Using
                (x + a)(x + b) = x2 + (a + b) + ab,
                we have:
                (x + 8)(x – 10) = x2 + [8 + (–10)]x + [8 × (–10)]
                = x2 + [–2]x + [–80]
                = x2 + 2x – 80
         (iii)   (3x + 4)(3x – 5):
                ∴ Using the identity
                (x + a)(x + b) = x2 + (a + b)x + ab,
                we have:
                (3x + 4)(3x – 5) = (3x)2 + [4 + (–5)]3x + [4 × (–5)]
                = 9x2 + [–1]3x + [–20]
                = 9x2 – 3x – 20
         (iv)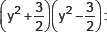   
                Using the identity
                (a + b)(a – b) = a2 – b2, we have:
         (v)   (3 – 2x)(3 + 2x):
                Using the identity
                (a + b)(a – b) = a2 – b2, we have:
                (3 – 2x)(3 + 2x) = (3)2 – (2x)2
                = 9 – 4x2
2.  Evaluate the following products without multiplying directly:
         (i)   103 × 107
         (ii)   95 × 96
         (iii)   104 × 96
Ans. (i)   We have 103 × 107 = (100 + 3)(100 + 7)
                = (100)2 + (3 + 7) × 100 + (3 × 7)
                [Using (x + a)(x + b) = x2 + (a + b)x +ab]
                = 10000 + (10) × 100 + 21
                = 10000 + 1000 + 21
                = 11021
         (ii)   We have 95 × 96 = (100 – 5)(100 – 4)
                = (100)2 + [(–5) + (–4)] × 100 + [(–5) × (–4)]
                [Using (x + a)(x + b) = x2 + (a + b)x +ab]
                = 10000 + [–9] × 100 + 21
                = 10000 + (–900) + 20
                = 9120
         (iii)   We have 104 × 96 = (100 + 4)(100 – 4)
                = (100)2 – (4)2
                [Using (a + b)(a – b) = a2 – b2]
                = 10000 – 16
                = 9984
3.  Factorise the following using appropriate identities:
         (i)   9x2 + 6xy + y2
         (ii)   4y2 – 4y + 1
         (iii)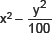   
Ans. (i)   We have 9x2 + 6xy + y2
                = (3x)2 + 2(3x)(y) + (y)2
                = (3x + y)2
                [Using a2 + 2ab + b2 = (a + b)2]
                = (3x + y)(3x + y)
         (ii)   We have 4y2 + 4y + 1
                = (2y)2 – 2(2y)(1) + (1)2
                = (2y – 1)2
                [∴ a2 – 2ab + b2 = (a – b)2]
                = (2y – 1)(2y – 1)
          
                [Using a2 – b2 = (a + b)(a – b)]
4.  Expand each of the following using suitable identities:
         (i)   (x + 2y + 4z)2
         (ii)   (2x – y + z)2
         (iii)   (–2x + 3y + 2z)2
         (iv)   (3a – 7b – c)2
         (v)   (–2x + 5y – 3z)2
       
Ans. (i)   (x + 2y + 4z)2
                We have
                (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
                ∴ (x + 2y + 4z)2 = (x)2 + (2y)2 + (4y)2 + 2(x)(2y) + 2(2y)(4z) + 2(4z)(x)
                = x2 + 4y2 + 16z2 + 4xy + 16yz + 8zx
         (ii)   (xx – y + z)2
                Using
                (x + y + z)2= x2 + y2 + z2 + 2xy + 2yz + 2zx,
                we have
                (2x – y + z)2 = (2x)2 + (–y)2 + (z)2 + 2(2x)(–y) + 2(–y)(z) + 2(z)(2x)
                = 4x2 + y2 + z2 – 4xy – 2yz + 4zx
         (iii)   (–2x + 3y + 2z)2
                Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx, we have
                (–2x + 3y + 2z)2 = (–2x)2 + (3y)2 + (2z)2 + 2(–2x)(3y) + 2(3y)(2z) + 2(2z)(–2x)
                = 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx
         (iv)   (3a – 7b – c)2
                Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx, we have
                (3a – 7b – c)2 = (3a)2 + (–7b)2 + (–c)2 + 2(3a)(–7b) + 2(–7b)(–c) + 2(–c)(3a)
                = 9a2 + 49b2 + c2 + (–42ab) + (14bc) – 6ca
                = 9a2 + 49b2 + c2 – 42ab + 14bc – 6ca
         (v)   (–2x + 5y – 3z)2
                Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx, we have
                ∴ (–2x + 5y – 3z)2 = (–2x)2 + (5y)2 + (–3z)2 + 2(–2x)(5y) + 2(5y)(–3z) + 2(–3z)(–2x)
                = 4x2 + 25y2 + 9z2 + [–20xy] + [–30yz] + [12zx]
                = 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12zx
         
                Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx, we have
                
5.  Factorise:
        
Ans. (i)   4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz
                = (2x)2 + (3y)2 + (–4z)2 + 2(2x)(3y)
                + 2(3y)(–4z) + 2(–4z)(2x)
                          [Using Identity V]
                = (2x + 3y – 4z)2
                = (2x + 3y – 4z)(2x + 3y – 4z)
         
6.  Write the following cubes in expanded form:
         (i)   (2x + 1)3
         (ii)   2a – 3b)3
         (iii)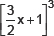   
         (iv)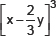   
Ans. Using Identity VI and Identity VII, we have
                (x + y)3 = x3 + y3 + 3xy (x + y), and
                (x + y)3 = x3 + y3 + 3xy (x – y).
         (i)   (2x + 1)3 = (2x)3 + (1)3 + 3(2x)(1)
                [(2x) + (1)]
                       = 8x3 + 1 + 6x[2x + 1]
                [Using Identity VI]
                       = 8x3 + 1 + 12x2 + 6x
                       = 8x3 + 12x2 + 6x + 1
         (ii)   (2a – 3b)3 = (2a)3 – (3b)3 – 3(2a)(3b)
                [(2a) + (3b)]
                 = 8a3 – 27b3 – 18ab[2a – 3b]
                [Using Identity VII]
                 = 8a3 – 27b3 – [36a2b – 54ab2]
                 = 8a3 – 27b3 – 36a2b + 54ab2
         
                 
         
7.  Evaluate the following using suitable identities:
         (i)   (99)3
         (ii)   (102)3
         (iii)   (998)3
Ans. (i)   (99)3
                We have 99 = 100 – 1
                ∴ 993 = (100 – 1)3
                = 1003 – 13 – 3(100)(1)(100 – 1)
                = 1000000 – 1 – 30000 + 300
                = 100300 – 30001
                = 970299
         (ii)   (102)3
                We have 102 = 100 + 2
                (102)3 = (100 + 2)3
                = (100)3 + (2)3 + 3(100)(2)[100 2 1]
                = 1000000 + 8 + 600[100 + 2]
                = 1000000 + 8 + 60000 + 1200
                = 1061208
         (ii)   (998)3
                 We have 998 = 100 – 2
                ∴ (999)3 = (1000 – 2)3
                = (1000)3 – (2)3 – 3(1000)(2)[1000 – 2]
                = 10000000 – 8 – 6000[1000 – 2]
                = 10000000 – 8 – 600000 – 12000
                = 994011992
8.  Factorise each of the following:
         (i)   8a3 + b3 + 12a2b + 6ab2
         (ii)   8a3 – b3 – 12a2b – 6ab2
         (iii)   27 – 125a3 – 135a + 225a2
         (iv)   64a3 – 27b3 – 144a2b + 108ab2
Ans. (i)   8a3 + b3 + 12a2b + 6ab2
                = (2a)3 + (b)3 + 6ab(2a + b)
                = (2a)3 + (b)3 + 3(2a)(b)(2a + b)
                = (2a + b)3              [Using Identify VI]
                = (2a + b)(2a + b)(2a + b)
         (ii)   8a3 – b3 – 12a2b – 6ab2
                = (2a)3 – (b)3 – 3(2a)(b)(2a – b)
                = (2a – b)3              [Using Identify VII]
                = (2a – b)(2a – b)(2a – b)
         (iii)   27 – 125a3 – 135a + 225a2
                = (3)3 – (5a)3 – 3(3)(5a)[3 – 5a]
                = (3 – 5a)3              [Using Identify VII]
                = (3 – 5a)(3 – 5a)(3 – 5a)
         (iv)   64a3 – 27b3 – 144a2b + 108ab2
                = (4a)3 – (3b)3 – 3(4a)(3b)[4a – 3b]
                = (4a – 3b)3              [Using Identify VII]
                = (4a – 3b)(4a – 3b)(4a – 3b)
         
9.  Verify:
         (i)   x3 + y3 = (x + y)(x2 – xy + y2)
         (ii)   x3 – y3 = (x – y)(x2 + xy + y2)
Ans. (i)   R.H.S. = (x + y)(x2 – xy + y2)
                = x(x2 – xy + y2) + y(x2 – xy + y2)
                = x3 – x2y + xy2 + x2y – xy2 + y3
                = x3 + y3
                = L.H.S
         (ii)   R.H.S. = (x – y)(x2 + xy + y2)
                = x(x2 + xy + y2) – y(x2 + xy + y2)
                = x3 + x2y + xy2 – x2y – xy2 – y3
                = x3 – y3
                = L.H.S
10.  Factorise each of the following:
         (i)   27y3 + 125z3
         (ii)   64m3 – 343n3
Remember
         I.   x3 + y3 = (x + y)(x2 + y2 – xy)
         II.   x3 – y3 = (x – y)(x2 + y2 + xy)
Ans. (i)   Using the identity
                x3 + y3 = (x + y)(x2 + – xy + y2), we have
                27y3 + 125z3 = (3y)3 + (5z)3
                = (3y + 5z)[(3y)2 – (3y)(5z) + (5z)2]
                = (3y + 5z)(9y2 – 15yz + 25z2)
         (ii)   Using the identity
                x3 – y3 = (x – y)(x2 + xy + y2), we have
                64m3 – 343n3 = (4m)3 – (7n)3
                = (4m – 7n)[(4m)2 + (4m)(7n) + (7n)2]
                = (4m + 7n)(16m2 + 28mn + 19n2)
11.  Factorise 27x3 + y3 + z3 – 9xyz.
Ans. Remember
                x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2
                – xy – yz – zx)
                We have
                27x3 + y3 + z3 – 9xyz = (3x)3 + (y)3 + (z)3
                – 3(3x)(y)(z)
                ∴ Using the identity
                x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2
                – xy – yz – zx), we have
                (3x)3 + y3 +z3 – 3(3x)(y)(z)
                = (3x + y +z)[(3x)2 + y2 + z2 – (3x × y)
                                                    – (y × z) – (z × 3x)]
                = (3x + y +z)(9x2 + y2 + z2 – 3xy – yz – 3zx)
12.  Verify that
13.  If x + y + z = 0, show that x3 + y3 + z3 = 3xyz.
Ans. Ans. Since x + y + z = 0
                ∴ x + y = –z
                or (x + y)3 = (–z)3
                or x3 + y3 + 3xy(x + y) = –z3
                or x3 + y3 + 3xy(–z) = –z3
                [ x + y = (–z)]
                or x3 + y3 – 3xy = –z3
                or (x3 + y3 + z3) – 3xy = 0
                or (x3 + y3 + z3) = 3xy
                Hence,
                         If x + y + z = 0, then (x3 + y3 + z3 = 3xy.
14.  Without actually calculating the cubes, find the value of each of the following:
         (i)   (–12)3 + (7)3 + (5)3
         (ii)   (28)3 + (–15)3 + (–13)3
Ans. (i)   (–12)3 + (7)3 + (5)3
                Let x = –12, y = 7 and z = 5
                Then x + y + z = –12 + 7 + 5 = 0
                We know that if
                x + y + z =0, then x3 + y3 + z3 = 3xyz.
                ∴ (–12)3 + (7)3 + (5)3 = 3[(–12)(7)(5)]
                [∴ (–12) + 7 + 5 = 0]
                = 3[–420]
                = –1260
                Thus, (–12)3 + (7)3 + (5)3 = –1260
         (ii)   (28)3 + (–15)3 + (–13)3
                Let x = 28, y = –15 and z = –13
                ∴ x + y + z =0, then x3 + y3 + z3 = 3xyz.
                We know that if
                x + y + z =0, then x3 + y3 + z3 = 3xyz.
                (28)3 + (–15)3 + (–13)3 = 3(28)(–15)(–13) [28 + (–15) + (–13) = 0]
                = 3(5460)
                = 16380
                Thus, (28)3 + (–15)3 + (–13)3 = 1638
15.  Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
Area: 25a – 35a 2 + 12 Area: 35y2 + 13y – 12
                        (i)                                        (ii)
Remember
                Area of a rectangle = (Length) × (Breadth)
Ans. (i)   Area = 25a2 – 35a + 12
                We have to factorise the polynomial:
                25a2 – 35a + 12
                Splitting the co-efficient of a, we have
                –35 = (–20) + (–15)
                [∴ 25 × 12 = 300 and (–20) × (–15) = 300]
                = 5a(5a – 4) – 3(5a – 4)
                = (5a – 4)(5a – 3)
                Thus, the possible length and breadth are                (5a –3) and (5a – 4).
         (ii)   Area = 35y2 + 13y – 12
                 We have to factorise the polynomial:
                 35y2 + 13y – 12
                 Splitting the middle term, we get
                 13y = 28y – 15y
                [∴ 28 × (–15) = –420 and –12 × 35 = –420]
                ∴ 35y2 + 13y – 12 = 35y2 + 28y – 15y – 12
                 = 7y(5y + 4) – 3(5y + 4)
                 = (5y + 4)(7y – 3)
                 Thus, the possible length and breadth are                 (7y – 3) and (5y + 4).
16.  What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
         (i)   Volume: 3x – 122 x
         (ii)   Volume: 12ky2 + 18ky – 12k
Remember
          Volume of a cuboid = (Length) × (Breadth) × (Height)
Ans. (i)   Volume = 3x2 – 12x
                 On factorising 3x2 – 12x, we have
                 3x2 – 12x = 3[x2 – 4x]
                 = 3 × [x(x – 4)]
                 = 3 × x × (x – 4)
                 ∴The possible dimensions of the cuboid are: 3, x and (x – 4) units.
         (ii)   Volume = 12ky2 + 8ky – 20k
                 We have
                 12ky2 + 8ky – 20k = 4[3ky2 + 2ky – 5k]
                 = 4[2(3y2 + 2y – 5]
                 (Splitting the middle term)
                 = 4k[3y(y – 1) + 5(y – 1)]
                 = 4k[(3y + 5)(y – 1)]
                 = 4k × (3y + 5) × (y – 1)
                 Thus, the possible dimensions are:
                 4k, (3y + 5) and (y – 1) units.