Polynomials-Sample Papers
Test For Polynomials
Class 9th
Chapter 2- Polynomials
Time: 1 Hour
Marks: 30
Question 1
( 2.0 marks)
The polynomials P(t) = 4t3 - st2 + 7 and Q(t) = t2 + st + 8 leave the same remainder when divided by (t - 1). Find the value of s.
Question 2
( 2.0 marks)
Find the value of k for which the cubic polynomial 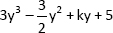 is exactly divisible by
is exactly divisible by 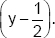
Question 3
( 2.0 marks)
Verify whether the indicated numbers are zeroes of their corresponding polynomials.
(a) Q(s) = -4s3 + 7s2 - 24; s = -4 and 1
1 marks
(b) 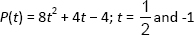
1 marks
Question 4
( 2.0 marks)
If x = -2 is a root of the polynomial P(x) = -2x4 - 7x3 - 3x2 - tx - 10, then find the value of t.
Question 5
( 3.0 marks)
State whether the following statements are true or false. Give reasons to justify your answers.
(a) The degree of polynomial -5x5 - 6x4 - 8x2 is 4.
1 marks
(b) The algebraic expression 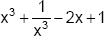 is a polynomial.
is a polynomial.
1 marks
(c) The polynomial 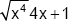 is a quadratic trinomial.
is a quadratic trinomial.
1 marks
Question 6
( 3.0 marks)
Using the long division method, determine the remainder when the polynomial 4x5 + 2x4 - x3 + 4x2 - 7 is divided by (x - 1).
Question 7
( 3.0 marks)
Evaluate the following products using algebraic identities.
(a) 9933
(b) 10023
Question 8
(4.0 marks)
If 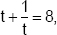 then find the value of
then find the value of 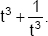
Question 9
(3.0 marks)
Using a suitable identity, determine the value of A) (17)3 + (-12)3 + (-5)3 and B) 64m3- 343n3
Question 10
(6.0 marks)
Factorise:
A) 2y3 - 4y2 - 2y + 4
B) 2x2 + 7x + 3
C) x3 + 13x2 + 32x + 20
