Quadrilaterals-NCERT Solutions
Class IX Math
NCERT Solution for Quadrilaterals
NCERT Solution for Quadrilaterals
NCERT TEXTBOOK QUESTIONS SOLVED
EXERCISE: 8.1 (Page 146)
Q1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : quadrilateral.
Sol: Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
∵ Sum of all the angles of quadrilateral = 360°
∴ 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360°
∴ 3x = 3 × 12° = 36°
5x = 5 × 12°= 60°
9x = 9 × 12° = 108°
13x = 13 × 12° = 156°
⇒ The required angles of the quadrilateral are 36°, 60°, 108° and 156°.
Q2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Sol: A parallelogram ABCD such that AC = BD In ΔABC and ΔDCB,
AC = DB
[Given]
AB = DC
[Opposite sides of a parallelogram]
BC = CB
[Common]
ΔABC = ΔDCB
[SSS criteria]
∴Their corresponding parts are equal.
⇒∠ABC = ∠DCB
...(1)
∵AB || DC and BC is a transversal.
[∵ ABCD is a parallelogram]
∴∠ABC + ∠DCB = 180°
...(2)
From (1) and (2), we have
∠ABC = ∠DCB = 90°
i.e. ABCD is parallelogram having an angle equal to 90°.
∴ABCD is a rectangle.
Q3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Sol: We have a quadrilateral ABCD such that the diagonals AC and BD bisect each other at right angles at O.
∴ In ΔAOB and ΔAOD, we have
AO = AO
[Common]
OB = OD
[Given that O in the mid-point of BD]
∠AOB = ∠AOD
[Each = 90°]
ΔAOB ≌ ΔAOD
[SAS criteria]
Their corresponding parts are equal.
AB = AD
...(1)
Similarly,
AB = BC
...(2)
BC = CD
...(3)
CD = AD
...(4)
∴ From (1), (2), (3) and (4), we have AB = BC CD = DA
Thus, the quadrilateral ABCD is a rhombus.
Q4. Show that the diagonals of a square are equal and bisect each other at right angles.
Sol: We have a square ABCD such that its diagonals AC and BD intersect at O.
(i) To prove that the diagonals are equal, i.e. AC = BD
In ΔABC and ΔBAD, we have
AB = BA
[Common]
BC = AD
[Opposite sides of the square ABCD]
∠ABC = ∠BAD
[All angles of a square are equal to 90°]
∴ΔABC ≌ ΔBAD
[SAS criteria]
⇒Their corresponding parts are equal.
⇒AC = BD
...(1)
(ii) To prove that 'O' is the mid-point of AC and BD.
∵ AD || BC and AC is a transversal.
[∵ Opposite sides of a square are parallel]
∴∠1 = ∠3
[Interior alternate angles]
Similarly, ∠2 = ∠4
[Interior alternate angles]
Now, in ΔOAD and ΔOCB, we have
AD = CB
[Opposite sides of the square ABCD]
∠1 = ∠3
[Proved]
∠2 = ∠4
[Proved
ΔOAD ≌ ΔOCB
[ASA criteria]
∴Their corresponding parts are equal.
⇒OA = OC and OD = OB
⇒O is the mid-point of AC and BD, i.e. the diagonals AC and BD bisect each other at O.
...(2)
(iii) To prove that AC 1 BD.
In ΔOBA and ΔODA, we have
OB = OD
[Proved]
BA =DA
[Opposite sides of the square]
OA = OA
[Common]
∴
ΔOBA ≌ ΔODA
[SSS criteria]
⇒Their corresponding parts are equal.
⇒ ∠AOB = ∠AOD
But ∠AOB and ∠AOD form a linear pair.
∠AOB + ∠AOD = 180°
∠AOB = ∠AOD = 90°
⇒AC ⊥ BD
...(3)
From (1), (2) and (3), we get AC and BD are equal and bisect each other at right angles.
Q5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Sol: We have a quadrilateral ABCD such that ��O�� is the mid-point of AC and BD. Also AC ⊥ BD.
Now, in ΔAOD and ΔAOB, we have
AO = AO
[Common]
OD = OB
[∵ O is the mid-point of BD]
∠AOD = ∠AOB
[Each = 90°]
∴ ΔAOD ≌ ∠AOB
[SAS criteria]
∴Their corresponding parts are equal.
⇒ AD = AB
...(1)
Similarly, we have
AB = BC
...(2)
BC = CD
...(3)
CD = DA
...(4)
From (1), (2), (3) and (4) we have: AB = BC = CD = DA
∴Quadrilateral ABCD is having all sides equal.
In ΔAOD and ΔCOB, we have
AO = CO
[Given]
OD = OB
[Given]
∠AOD = ∠COB
[Vertically opposite angles]
∴
ΔAOD ≌ ΔCOB
⇒Their corresponding pacts are equal.
⇒ ∠1 = ∠2
But, they form a pair of interior alternate angles.
∴AD || BC
Similarly, AB || DC
∴ ABCD is' a parallelogram.
∵ Parallelogram having all of its sides equal is a rhombus.
∴ ABCD is a rhombus.
Now, in ΔABC and ΔBAD, we have
AC = BD
[Given]
BC = AD
[Proved]
AB = BA
[Common]
ΔABC ≌ ΔBAD
[SSS criteria]
Their corresponding angles are equal.
∠ABC = ∠BAD
Since, AD || BC and AB is a transversal.
∴∠ABC + ∠BAD = 180°
[Interior opposite angles are supplementary]
i.e. The rhombus ABCD is having one angle equal to 90°.
Thus, ABCD is a square.
Q6. Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
Sol: We have a parallelogram ABCD in which diagonal AC bisects ∠A.
⇒ ∠DAC = ∠BAC
(i) To prove that AC bisects ∠C.
∵ABCD is a parallelogram.
∴AB || DC and AC is a transversal.
∴∠l = ∠3
[Alternate interior angles] ...(1)
Also, BC || AD and AC is a transversal.
∴∠2 = ∠4
[Alternate interior angles] ...(2)
But AC bisects ∠A.
[Given]
∴∠1 = ∠2
...(3)
From (1), (2) and (3), we have
∠3 = ∠4
⇒AC bisects ∠C.
(ii) To prove ABCD is a rhombus.
In ΔABC, we have ∠1 = ∠4
[∵∠1 = ∠2 = ∠4]
⇒
BC = AB
Sides opposite to equal angles are equal] ...(4)
Similarly,
AD = DC
...(5)
But ABCD is a parallelogram
[Given]
AB = DC
[Opposite sides of a parallelogram] ...(6)
From (4), (5) and (6), we have
AB = BC = CD = DA
Thus, ABCD is a rhombus.
Q7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Sol: ABCD is a rhombus.
∴ AB = BC = CD = AD
Also, AR || CD an AD || BC
Now, AD = CD ⇒∠1 = ∠2 ...(1)
[Angles opposite to equal sides-are equal]
Also, CD II AB
[Opposite sides of the parallelogram]
∴ ∠1 = ∠3
and AC is AC is transversal.
∴ ∠1 = ∠3
From (1) and (2), we have
∠2 = ∠3 and ∠1 = ∠4
⇒AC bisects ∠C as well as ∠A.
Similarly, we prove that BD bisects ∠B as well as ∠D.
Q8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Sol: We have a rectangle ABCD such that AC bisects ∠A as ∠C.
i.e. ∠1 = ∠4 and ∠2 = ∠3 ...(1)
(i) Since, rectangle is a parallelogram.
∴ ABCD is a parallelogram.
⇒AB || CD and AC is a transversal.
∴∠2 = ∠4
[Alternate interior angles] ...(2)
From (1) and (2), we have
∠3 = ∠4
⇒AB = BC
[ ∵ Sides opposite to equal angles in ΔABC are equal.]
∴AB = BC = CD = AD
⇒ABCD is a rectangle having all of its sides equal.
∴ABCD is a square.
(ii) Since, ABCD is a square, and diagonals of a square bisect the opposite angles.
∴ BD bisects ∠B as well as ∠D.
Q9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:
(i) ΔAPD ≌ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≌ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Sol: We have parallelogram ABCD. BD is a diagonal and ‘P’ and ‘Q’ are such that
PD = QB
[Given]
(i) To prove that ΔAPD ≌ ΔCQB
∵ AD || BC and BD is a transversal.
[∵ABCD is a parallelogram.]
∴∠ADB = ∠CBD
[Interior alternate angles]
⇒∠ADP = ∠CBQ
Now, in ΔAPD and ΔCQB, we have
AD =CB
[Opposite side of the parallelogram]
PD = QB
[Given]
∠CBQ = ∠ADP
[Proved]
∴ Using SAS criteria, we have
ΔAPD ≌ ΔCQB
(ii) To prove that AP = CQ
Since ΔAPD ≌ ΔCQB
[Proved]
∴ Their corresponding parts are equal.
⇒AP = CQ
(iii) To prove that ΔAQB ≌ ΔCPD.
AB || CD and BD is a transversal.
[ ∵ ABCD is a parallelogram.]
∴∠ABD = ∠CDB
⇒∠ABQ = ∠CDP
Now, in ΔAQB and ΔCPD, we have
QB = PD
[Given]
∠ABQ = ∠CDP
[Proved]
AB = CD
[Opposite sides of parallelogram ABCD]
∴ΔAQB ≌ ΔCPD
[SAS criteria]
(iv) To prove that AQ = CP.
Since ΔAQB ≌ ΔCPD
[Proved]
∴Their corresponding parts are equal.
⇒ AQ = CP.
(v) To prove that APCQ is a parallelogram.
Let us join AC.
Since, the diagonals of a || gm bisect each other
∴AO = CO
and BO = DO
⇒(BO – BQ) = (DO – DP)
[∵ BQ = DP (Given)]
⇒QO = PO
...(2)
Now, in quadrilateral APCQ, we have
AO = CO and QO = PO
i.e. AC and QP bisect each other at O.
⇒APCQ is a parallelogram.
Q10. ABCD is a parallelogram and AP and perpendiculars from vertices A and C on diagonal BD (see Show that
(i) ΔAPB ≌ ΔCQD
(ii) AP = CQ
Sol: (i) In ΔAPB and ΔCQD, we have
∠APB = ∠CQD [90° each]
AB = CD
[Opposite sides of parallelogram ABCD]
∠ABP = ∠CDQ
⇒Using AAS criteria, we have
∠APB ≌ ΔCQD
(ii) Since, ΔAPB ≌ ΔCQD
∴ Their corresponding parts are equal.
⇒AP = CQ
Q11. In ΔABC and ΔDEF, AB = DE, AB || DE, and BC || EF. vertices A, B and C are joined to vertices F respectively (see figure). Show that
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BEFC is a parallelogram.
(iii) AD || CF and AD = CF.
(iv) quadrilateral ACFD is a parallelogram.
(v) AC = DF
(vi) ΔABC ≌ ΔDEF:
Sol: (i) To prove that ABED is a parallelogram.
Since “A quadrilateral is a parallelogram if a pair of equal length.”
Now
AB = DE
[Given]
AB || DE
[Given]
i.e. ABED is a quadrilateral in which a pair of opposite and of equal length.
∴ ABED is a parallelogram.
(ii) To prove that BECF is a parallelogram.
∵
BC = EF
[Given]
and
BC || EF
[Given]
i.e. BECF is a quadrilateral in which a pair of opposite sides (BC and EF) is parallel and of equal length.
∴ BECF is a parallelogram.
(iii) To prove that AD || CF and AD = CF
∵ABED is a parallelogram.
[Proved]
∴ Its opposite sides are parallel and equal.
⇒ AD || BE and AD = BE
...(1)
Also BEFC is a parallelogram.
[Proved]
∴ BE || CF and BE = CF
[∵Opposite sides of a parallelogram are parallel and equal] ...(2)
From (1) and (2), we have AD || CF and AD = CF
(iv) To prove that ACFD is a parallelogram.
∵ AD || CF
[Proved]
and AD = CF
[Proved]
i.e. In quadrilateral ACFD, one pair of opposite sides (AD and CF) is parallel and of equal length.
∴ Quadrilateral ACFD is a parallelogram.
(v) To prove that AC = DE.
∵ACFD is a parallelogram.
[Proved]
∴ Its opposite sides are parallel and of equal length.
i.e. AC = DF
(vi) To prove that ΔABC ≌ ΔDEF
In ΔABC and ΔDEF, we have:
AB = DE
[Opposite sides of a parallelogram]
BC = EF
[Opposite sides of a parallelogram]
AC = DF
[Proved]
∴ Using SSS criteria, we have ΔABC ≌ ΔDEF.
Q12. ABCD is a trapezium in which AB II CD and AD = BC (see figure).
Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∠ABC ≌ ∠BAD
(iv) Diagonal AC = Diagonal BD
Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.
Sol: We have AB || CD and AD = BC
(i) To prove that ∠A = ∠B.
Produce AB to E and draw CE || AD.
∴
AB || DC
⇒ AE || DC
[Given]
Also
AD || CE
∴AECD is a parallelogram.
⇒
AD = CE
[opposite sides of the parallelogram AECD]
But
AD = BC
[Given]
∴
BC = CE
BC = CE
Now, in ΔBCE, we have
BC = CE
⇒
∠CBE = ∠CEB
...(1)
[∵ Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180°
[Linear pair] ...(2)
and ∠A + ∠CEB = 180°
[∵Adjacent angles of a parallelogram are supplementary]
...(3)
From (2) and (3), we get
∠ABC + ∠CBE = ∠A + ∠CEB
But
∠CBE = ∠CEB
∴
∠ABC = ∠A
or
∠B = ∠A
or
∠A = ∠B
(ii) To prove that ∠C = ∠D.
AB || CD and AD is a transversal.
∠A + ∠D = 180°
[Sum of interior opposite angles]
Similarly, ∠B + ∠C = 180°
⇒∠A + ∠D = ∠B + ∠C
But ∠A = ∠B
[Proved]
∴∠C = ∠D
(iii) To prove ΔABC ≌ ΔBAD
In ΔABC and ΔBAD, we have
AB = BA
[Common]
BC = AD
[Given]
∠ABC = ∠BAD
[Proved]
∴ΔABC ≌ ΔBAD
[Using SAS criteria]
(iv) To prove that diagonal AC = diagonal BD
ΔABC ≌ ΔBAD
[Proved]
∴ Their corresponding parts are equal.
⇒the diagonal AC = the diagonal BD.
NCERT TEXTBOOK QUESTIONS SOLVED
EXERCISE 8.2 (Page 150)
Q1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that.
(i) SR || AC and 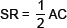
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Sol: We have Pas the mid-point of AB, Q as the mid-point of BC,
(i) To prove that 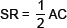 and SR || AC
and SR || AC
R as the mid-point of CD, S as the mid-point of DA, and AC as the diagonal of quadrilateral ABCD.
In ΔACD, we have
S as the mid-point of AD,
R as the mid-point of CD.
∵ The line segment joining the mid-point of any two sides of a triangle is parallel to the third side and half of it.
(ii) To prove that PQ = SR.
In ΔABC, we have
P is the mid-point of AB,
Q is the mid-point of BC.
From (1) and (2), PQ = SR
(iii) To prove that PQRS is a parallelogram.
In ΔABC, P and Q are the mid-points of AB and BC.
In ΔACD, S and R are the mid-points of DA and CD.
From (3) and (4), we get
⇒ PQ = SR and PQ || SR
i.e. One pair of opposite sides in quadrilateral PARS is equal and parallel.
∴ PQRS is a parallelogram.
Q2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Sol: We have P as the mid-point of AB, Q as the mid-point of BC, R as the mid-point of CD, S as the mid-point of DS.
We have to prove that PQRS is a rectangle. Let us join AC.
∵ In DABC, P and Q are the mid-points of AB and BC.
Also in ΔADC, R and S are the mid-points of CD and DA.
From (1) and (2), we get
⇒ PQ = SR and PQ || SR
i.e. One pair of opposite sides of quadrilateral PQRS is equal and parallel.
∴ PQRS is a parallelogram.
Now, in ΔERC and ΔEQC,
∠1 = ∠2
[ ∵The diagonal of a rhombus bisects the opposite angles]
CR = CQ
[Each is equal to  of a side of rhombus]
of a side of rhombus]
CE = CE
[Common]
ΔERC ≌ ΔEQC
[SAS criteria]
⇒∠3 = ∠4
[c.p.c.t.]
But ∠3 + ∠4 = 180°
[Linear pair]
⇒ ∠3 = ∠4 = 90°
But ∠5 = ∠3
[Vertically opposite angles]
∠5 = 90°
PQ || AC ⇒ PQ || EF
∴PQEF is a quadrilateral having a pair of opposite sides parallel and one of the angles is 90°.
∴PQEF is a rectangle.
⇒∠RQP = 90°
∴One angle of parallelogram PQRS is 90°.
Thus, PQRS is a rectangle.
Q3. ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Sol: In a rectangle ABCD, P is the mid-point of AB, Q is the mid-point of BC, R is the mid-point of CD, S is the mid-point of DA AC is the diagonal.
From (1) and (2), we get
PQ = SR and PQ || SR
Similarly, by joining BD, we have
PS = QR and PS || QR
i.e. Both pairs of opposite sides of quadrilateral PQRS are equal and parallel.
∴ PQRS is a parallelogram.
Now, in ΔPAS and ΔPBQ,
∴Their corresponding parts are equal.
⇒
PS = PQ
Also
PS = QR
[Proved]
and
PQ = SR
[Proved]
PQ = QR = RS = SP
i.e. PQRS is a parallelogram having all of its sides equal.
⇒PQRS is a rhombus.
Q4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid point of BC.
Sol: In trapezium ABCD, AB || DC. E is the mid-point of AD. EF is drawn parallel to AB. We have to prove that F is the mid-point of BC.
Join BD.
In ΔDAB,
∵ E is the mid-point of AD
and EG || AB
∴ Using the converse of mid-point theorem, we get that G is the mid-point BD.
Again in ΔBDC
∵G is the mid-point of BD
[Proved]
GF || DC
[ ∵AB || DC and EF || AB and GF is a part of EF]
∴ Using the convene of the mid-point theorem, we get that F is the mid-point of BC.
Q5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
Sol: We have ABCD is a parallelogram such that:
E is the mid-point of AB and F is the mid-point of CD. Let us join the opposite vertices B and D.
Since, the opposite sides of a parallelogram are parallel and equal.
∴ AB || DC ⇒ AE || FC
...(1)
Also AB = DC
From (1) and (2), we can say that AECF is quadrilateral having a pair of the opposite sides as parallel and equal.
∴ AEFC is a parallelogram.
⇒ AE || CF
Now, in ΔDBC,
F is the mid-point of DC
[Given]
and FP || CQ
[∵ AF || CE]
⇒ P is the mid-point of DQ
[Converse of mid-point theorem]
⇒ DP = PQ
...(3)
Similarly, in ΔBAP,
BQ = PQ
...(4)
∴ From (3) and (4), we have
DP = PQ = BQ
⇒ The line segments AF and EC trisect the diagonal BD.
Q6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Sol: A quadrilateral ABCD such that the mid-points of AB, BC, CD and DA are P, Q, R and S respectively,
we have to prove that diagonals of PARS are bisected at O.
Join PQ, QR, RS and SP. Let us also join PR and SQ.
Now, in AABC, we have P and Q as the mid-points of its sides AB and BC respectively.
⇒ PQRS is a quadrilateral having a pair of opposite sides (PQ and RS) as equal and parallel.
∴ PQRS is a parallelogram.
But the diagonals of a parallelogram bisect each other.
i.e. PR and SQ bisect each other.
Thus, the line segments joining the mid-points of opposite sides of a quadrilateral ABCD bisect each other.
Q7. ABC is a triangle, right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
Sol: We have a triangle ABC, such that ∠C = 90°
M is the mid-point of AB and MD || BC.
(i) To prove that D is the mid-point of AC.
In ΔACB, we have
M as the mid-point of AB.
[Given]
MD || BC
[Given]
∴ Using the converse of mid-point theorem, D is the mid-point of AC.
(ii) To prove that MD ⊥ AC.
[Given]
Since, MD || BC
and AC is a transversal.
∠MDA = ∠BCA
[Corresponding angles]
But
∠BCA = 90°
[Given]
∴
∠MDA = 90°
⇒
MD ⊥ AC.
(iii) To prove that CM = MA =  AB
AB
In ΔADM and ΔCDM, we have
∠ADM = ∠CDM
[Each = 90°]
MD = MD
[Common]
AD = CD
[∵M is the mid-point of AC (Proved)]
∴
ΔADM = ΔCDM
[SAS criteria]
⇒
MA = MC
[c.p.c.t.] ...(1)
∵M is the mid-point AB.
[Given]
∴ MA =  AB
AB
...(2)
From (1) and (2), we have
CM = MA =  AB
AB
