Polynomials-Important Questions

1.  If one zero of the polynomial 5z² + 13z – p is reciprocal of the other, then find p.

2.  If the product of two zeroes of polynomial 2x³ + 3x² – 5x – 6 is 3, then find its third zero.

3.  Find the polynomial of least degree which should be subtracted from the polynomial x4 + 2x³ – 4x² + 6x – 3 so that it is exactly divisible by x² – x + 1.

4.  Is polynomial y⁴ + 4y² + 5 have zeroes or not?

5.  Write a quadratic polynomial, sum of whose zeroes is 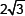and product is 5.

6.  Write the zeroes of the polynomial x² + 2x + 1.

7.  If the zeroes of the polynomial f(x) = x³ – 12x² + 39x + a are in AP, find the value of a.

8.  A polynomial g(x) of degree zero is added to the polynomial 2x³ + 5x² – 14x + 10 so that it becomes exactly divisible by 2x – 3. Find the g(x).

9.  Find the zeroes of the quadratic polynomial x² + 5x + 6 and verify the relationship between the zeroes and the coefficients.

10.  If the zeroes of polynomial x³ – ax² + bx – c are in AP then show that 2a³ – 9ab + 27c = 0

11.  If 1 and –1 are zeroes of polynomial Lx⁴ + Mx³ + Nx² + Rx + P, show that L + N + P = M + R = 0

12.  Draw graph of the function f(x) = –2x² + 4x.

13.  If x + a is a factor of the polynomial x² + px + q and x² + mx + n prove that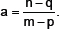

14.  Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time and product of its zeroes are 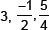respectively.

15.  Write cubic polynomial whose zeroes are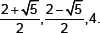

16.  α, β, γ are zeroes of cubic polynomial kx³ – 5x + 9.
          If α³ + β³ + γ³ = 27, find the value of k.

17.  α, β, γ are zeroes of cubic polynomial x³ – 12x² + 44x + c.
         If α, β, γ are in AP, find the value of c.

18.  Two zeroes of cubic polynomial ax³ + 3x² – bx – 6 are –1 and –2. Find the third zero and value of a and b.

19.  α, β, γ are zeroes of cubic polynomial x³ – 2x² + qx – r.
         If α + β = 0 then show that 2q = r.

20.  α, β, γ are zeroes of polynomial x³ + px² + qx + 2 such that α.
         β + 1 = 0. Find the value of 2p + q + 5.