Polynomials-MCQ
MULTIPLE CHOICE QUESTIONS
POLYNOMIALS
POLYNOMIALS
1. The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
(a) x2 + 3x – 2
(b) x2 – 2x + 3
(c) x2 – 3x + 2
(d) x2 – 3x – 2
2. If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a – 3b = 4
(a) a = –1, b = –2
(b) a = 2, b = 5
(c) a = 5, b = 2
(d) a = 2, b = 0
3. The number of zeroes that polynomial f(x) = (x – 2)2 + 4 can have is:
(a) 1
(b) 2
(c) 0
(d) 3
4. The zeroes of the polynomial f(x) = 4x2 – 12x + 9 are:
(a)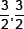 
(b)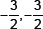 
(c) 3, 4
(d) –3, –4
5. If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as
(a) value of p(x)
(b) zero of p(x)
(c) constant term of p(x)
(c) none of these
6. If p(x) = ax + b, then zero of p(x)
(a) a
(b) b
(c)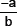 
(d)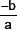 
7. Graph of a quadratic polynomial is a
(a) straight line
(b) circle
(c) parabola
(d) ellipse
8. Zeroes of a polynomial can be determined graphically. No. of zeroes of a polynomial is equal to no. of points where the graph of polynomial
(a) intersects y-axis
(b) intersects x-axis
(c) intersects y-axis or intersects x-axis
(d) none of these
9. If graph of a polynomial does not intersects the x-axis but intersects y-axis in one point, then no, of zeroes of the polynomial is equal to
(a) 0
(b) 1
(c) 0 or 1
(d) none of these
10. A polynomial of degree n has
(a) only 1 zero
(b) exactly n zeroes
(c) atmost n zeroes
(d) more than n zeroes
11. If p(x) = ax2 + bx + c, then 
is equal to
is equal to (a) 0
(b) 1
(c) sum of zeroes
(d) product of zeroes
12. If p(x) = ax2 + bx + c, then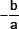 
is equal to
is equal to (a) 0
(b) 1
(c) product of zeroes
(d) sum of zeroes
13. If p(x) = ax2 + bx + c, and a + b + c = 0, then one zero
(a)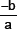 
(b) 
(c) 
(d) none of these
14. If p(x) = ax2 + bx + c and a + c = b, then one of the zeroes is
(a) 
(b) 
(c) 
(d) 
15. A quadratic polynomial whose one zero is 6 and sum of the zeroes is 0, is
(a) x2 – 6x + 2
(b) x2 – 36
(c) x2 – 6
(d) x2 – 3
